题目内容
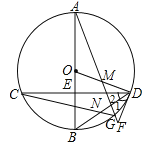
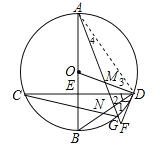
【题目】如图,在⊙O中,直径AB经过弦CD的中点E,点M在OD上,AM的延长线交⊙O于点G,交过D的直线于F,∠1=∠2,连结BD与CG交于点N.
(1)求证:DF是⊙O的切线;
(2)若点M是OD的中点,⊙O的半径为3,tan∠BOD=![]() ,求BN的长.
,求BN的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)根据切线的判定定理得出∠1+∠BDO=90°,即可得出答案;
(2)利用已知得出∠3=∠2,∠4=∠C,再利用相似三角形的判定方法得出即可;根据已知得出OE的长,进而利用勾股定理得出ED,AD,BD的长,即可得出CD,利用相似三角形的性质得出NB的长即可.
试题解析:解:(1)证明:∵直径AB经过弦CD的中点E,∴AB⊥CD, ![]() ,∴∠BOD=2∠2.
,∴∠BOD=2∠2.
∵∠1=∠2,∠BOD+∠ODE=90°,∴∠ODE+∠1+∠2=90°,∴∠ODF=90°,∴DF是⊙O的切线;
(2)解:∵AB是⊙O直径,∴∠ADB=∠FDO=90°,∴∠ADB﹣∠BDO=∠FDO﹣∠BDO,即∠3=∠1,∴∠3=∠2,∵∠4=∠C,∴△ADM∽△CDN;
∵⊙O的半径为3,即AO=DO=BO=3,在Rt△DOE中,tan∠BOD=![]() ,cos∠BOD=
,cos∠BOD=![]() ,∴OE=DOcos∠BOD=3×
,∴OE=DOcos∠BOD=3×![]() =1,由此可得:BE=2,AE=4,由勾股定理可得:DE=
=1,由此可得:BE=2,AE=4,由勾股定理可得:DE=![]() =
=![]() ,AD=
,AD=![]() =
=![]() ,BD=
,BD=![]() =
=![]() ,∵AB是⊙O直径,AB⊥CD,∴由垂径定理得:CD=2DE=
,∵AB是⊙O直径,AB⊥CD,∴由垂径定理得:CD=2DE=![]() ,∵△ACM∽△DCN,∴
,∵△ACM∽△DCN,∴![]() ,∵点M是DO的中点,DM=
,∵点M是DO的中点,DM=![]() AO=
AO=![]() ×3=
×3=![]() ,∴DN=
,∴DN=![]() =
= =
=![]() ,∴BN=BD﹣DN=
,∴BN=BD﹣DN=![]() =
=![]() .
.

【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/辆 | -1 | +3 | -2 | +4 | +7 | -5 | -10 |
本周总的生产量是多少辆?





