题目内容
6.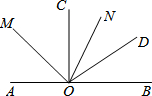 如图,∠AOC=90°,ON是锐角∠COD的角平分线,OM是∠AOD的角平分线,那么,∠MON=45°.
如图,∠AOC=90°,ON是锐角∠COD的角平分线,OM是∠AOD的角平分线,那么,∠MON=45°.
分析 根据ON是锐角∠COD的角平分线,OM是∠AOD的角平分线,得出∠AOM=∠MOD,∠CON=∠NOD,又∠AOC=90°即可得出∠AOM=∠MOD=45°+$\frac{1}{2}$∠COD.进而求出∠MON的度数.
解答 解:∵ON是锐角∠COD的角平分线,
∴∠CON=$\frac{1}{2}$∠COD,
∵ON是锐角∠COD的角平分线,
∴∠AOM=$\frac{1}{2}$∠AOD=$\frac{1}{2}$(∠AOC+∠COD)=45°+∠CON,
∴∠COM=∠AOC-∠AOM=90°-(45°+∠CON)=45°-∠CON,
∴∠MON=∠COM+∠CON=45°-∠CON+∠CON=45°.
故答案为:45°.
点评 本题考查了角平分线的定义,角的比较与运算,熟记角平分线的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.下列计算正确的是( )
| A. | x2•x4=x6 | B. | x2+x3=x5 | C. | (x2)3=x5 | D. | x10÷x2=x5 |
17.已知?ABCD中BC=8,点P是BC上的点,E、F分别是AP、DP的中点,点P在BC上从点B向点C移动,那么线段EF的长( )
| A. | 逐渐增大 | B. | 始终等于16 | C. | 始终等于4 | D. | 不能确定 |
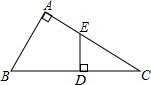 如图,在Rt△ABC中,∠A=90°,∠C=30°,D为斜边上的一点且BD=AB,过点D作BC的垂线,交AC于点E.若△CDE的面积为a,则四边形ABDE的面积为2a.
如图,在Rt△ABC中,∠A=90°,∠C=30°,D为斜边上的一点且BD=AB,过点D作BC的垂线,交AC于点E.若△CDE的面积为a,则四边形ABDE的面积为2a.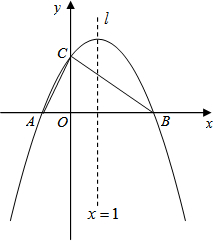 如图,在平面直角坐标系xOy中,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12).
如图,在平面直角坐标系xOy中,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12).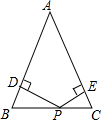 如图,在△ABC中,AB=AC=8,P是BC上任意一点,PD⊥AB,PE⊥AC,△ABC面积为4.
如图,在△ABC中,AB=AC=8,P是BC上任意一点,PD⊥AB,PE⊥AC,△ABC面积为4.