题目内容
已知△ABC与△DEF相似且面积之比为4：9，则△ABC与△DEF的对应边上的高线比为 ．
【答案】分析：由△ABC与△DEF相似且面积之比为4：9，可求得△ABC与△DEF相似比，即可求得△ABC与△DEF的对应边上的高线比．
解答：解：∵△ABC与△DEF相似且面积之比为4：9，
∴△ABC与△DEF相似比为2：3，
∴△ABC与△DEF的对应边上的高线比为2：3．
故答案为：2：3．
点评：本题考查对相似三角形性质．注意相似三角形面积的比等于相似比的平方与相似三角形对应高的比等于相似比．
解答：解：∵△ABC与△DEF相似且面积之比为4：9，
∴△ABC与△DEF相似比为2：3，
∴△ABC与△DEF的对应边上的高线比为2：3．
故答案为：2：3．
点评：本题考查对相似三角形性质．注意相似三角形面积的比等于相似比的平方与相似三角形对应高的比等于相似比．
练习册系列答案
相关题目
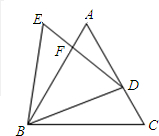如图，已知△ABC与△BDE都是等边三角形，点D在边AC上（不与A、C重合），DE与AB相交于点F．
如图，已知△ABC与△BDE都是等边三角形，点D在边AC上（不与A、C重合），DE与AB相交于点F．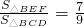
？
？