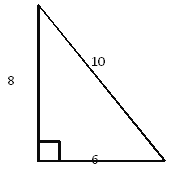
题目内容
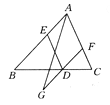
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE= ![]() ,则△ABC的面积为( )
,则△ABC的面积为( ) 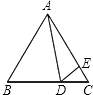
A.8 ![]()
B.15
C.9 ![]()
D.12 ![]()
【答案】C
【解析】解:∵△ABC是等边三角形,∠ADE=60°, ∴∠B=∠C=∠ADE=60°,AB=BC,
∵∠ADB=∠DAC+∠C,∠DEC=∠ADE+∠DAC,
∴∠ADB=∠DEC,
∴△ABD∽△DCE,
∴ ![]() ,
,
∵BD=4,CE= ![]() ,
,
设AB=x,则DC=x﹣4,
∴ ![]() ,
,
∴x=6,
∴AB=6,
过点A作AF⊥BC于F,
在Rt△ABF中,AF=ABsin60°=6× ![]() =3
=3 ![]() ,
,
∴S△ABC= ![]() BCAF=
BCAF= ![]() ×6×3
×6×3 ![]() =9
=9 ![]() .
.
故选C.
首先由△ABC是等边三角形,可得∠B=∠C=∠ADE=60°,又由三角形外角的性质,求得∠ADB=∠DEC,即可得△ABD∽△DCE,又由BD=4,CE= ![]() ,根据相似三角形的对应边成比例,即可求得AB的长,则可求得△ABC的面积.
,根据相似三角形的对应边成比例,即可求得AB的长,则可求得△ABC的面积.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目