题目内容
如图,⊙M过坐标原点O,分别交两坐标轴于A(1,O),B(0,2)两点,直线CD交x轴于点C(6,0),交y轴于点D(0,3),过点O作直线OF,分别交⊙M于点E,交直线CD于点F.
(1)∠CDO=∠BAO;
(2)求证:OE•OF=OA•OC;
(3)若OE= ,试求点F的坐标.
,试求点F的坐标.


证明:(1)如图:
∵C(6,0),D(0,3),
∴tan∠CDO= =
= =2,
=2,
∵A(1,O),B(0,2),
cot∠BAO= =2,
=2,
∴∠CDO=∠BAO,
(2)如图,连接AE,

由(1)知∠CDO=∠BAO,
∴∠OCD=∠OBA,
∵∠OBA=∠OEA,
∴∠OCD=∠OEA,
∴△OCF∽△OEA,
∴ =
=
∴OE•OF=OA•OC;
(3)由(2)得OE•OF=OA•OC,
∵OA=1,0C=6,OE= ,
,
∴OF═ =
= =2
=2
设F(x,y)
∴x2+y2=8,
∵直线CD的函数式为:y=﹣ x+3
x+3
∴组成的方程组为 ,
,
解得 或
或
∴F的坐标为:(2,2)或( ,
, ).
).

练习册系列答案
相关题目
如图图形中,是轴对称图形,但不是中心对称图形的是( )
|
| A. |
| B. |
| C. |
| D. |
|
如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=2,过点C作CD⊥AB,垂足为D,则CD的长为( )

|
|
|
| B. |
| C. | 1 | D. | 2 |
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )

|
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |




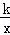 (x>0)的图象交于点A(2,1),与x轴交于点B.
(x>0)的图象交于点A(2,1),与x轴交于点B.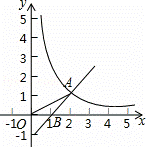
 点A3,顶点为P3,…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为( ).
点A3,顶点为P3,…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为( ).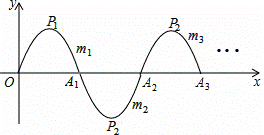
 A.
A.

 B.
B.
 D.
D.