题目内容
如图，已知二次函数y=x2+bx+c的图象经过点（-1，0），（1，-2），该图象与x轴的另一个交点为C，则AC长为________．
3
分析：先把点（-1，0），（1，-2）代入y=x2+bx+c，求得b，c，再令y=0，点C的坐标，再得出答案即可．
解答：∵二次函数y=x2+bx+c的图象经过点（-1，0），（1，-2），
∴
，
解得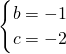
，
∴抛物线的解析式为y=x2-x-2，
令y=0，得x2-x-2=0，
解得x1=-1，x2=2，
∴C（2，0）
∴AC=2-（-1）=3．
故答案为3．
点评：本题考查了用待定系数法求二次函数的解析式、抛物线与x轴的交点问题以及两点间距离的求法，是基础知识要熟练掌握．
分析：先把点（-1，0），（1，-2）代入y=x2+bx+c，求得b，c，再令y=0，点C的坐标，再得出答案即可．
解答：∵二次函数y=x2+bx+c的图象经过点（-1，0），（1，-2），
∴
，解得
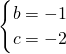，∴抛物线的解析式为y=x2-x-2，
令y=0，得x2-x-2=0，
解得x1=-1，x2=2，
∴C（2，0）
∴AC=2-（-1）=3．
故答案为3．
点评：本题考查了用待定系数法求二次函数的解析式、抛物线与x轴的交点问题以及两点间距离的求法，是基础知识要熟练掌握．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
三角形与△BOF相似？若存在，请求出P点的坐标；若不存在，请说明理由．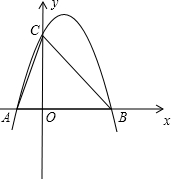
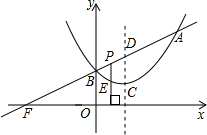
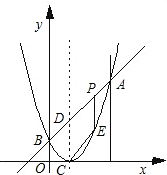如图，已知二次函数图象的顶点坐标为C（1，0），直线y=x+b与该二次函数的图象交于A、B两点，其中点A的坐标为（3，4），点B在y轴上．点P为线段AB上的一个动点（点P与A、B不重合），过点P作x轴的垂线与该二次函数的图象交于点E．
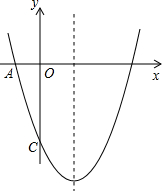如图，已知二次函数y=ax2-4x+c的图象与坐标轴交于点A（-1，0）和点C（0，-5）．
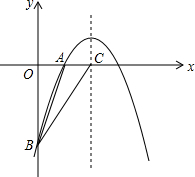（2012•衡水一模）如图，已知二次函数