题目内容
(本小题满分14分)设函数
(1)当
 时,求
时,求 的极值;
的极值;(2)当
 时,求
时,求 的单调区间;
的单调区间;(3)当
 时,对任意的正整数
时,对任意的正整数 ,在区间
,在区间 上总有
上总有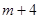 个数使得
个数使得 成立,试求正整数
成立,试求正整数 的最大值。
的最大值。
(1) ,没有极大值.
,没有极大值.
(2)综上,当 时,函数的单调递减区间为
时,函数的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,函数的单调递减区间为
时,函数的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,函数的单调递减区间为
时,函数的单调递减区间为 单调递增区间为
单调递增区间为
(3) 解析:
解析:
(1)先求出函数的定义域,再求出函数的导数,研究其单调性求出
其极值;(2)令 =0,得
=0,得 ,
, 比较
比较 与
与 的大小得
的大小得 和
和 的
的 范围,就得到了函数的单调区间;
范围,就得到了函数的单调区间;
(3)解本题的关键是要使在区间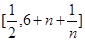 上总有
上总有 个数使得
个数使得 成立,只需
成立,只需
 即可。
即可。
解:(1)函数 的定义域为
的定义域为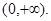 ……………………………………1分
……………………………………1分
当 时,
时, ,∴
,∴ ………………2分
………………2分
由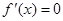 得
得
 随
随 变化如下表:
变化如下表:
故, ,没有极大值. …………………………4分
,没有极大值. …………………………4分
(2)由题意,
令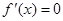 得
得 ,
, ………………………………………………6分
………………………………………………6分
若 ,由
,由 得
得 ;由
;由 得
得 …………7分
…………7分
若 ,①当
,①当 时,
时, ,
, 或
或 ,
, ;
;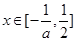 ,
,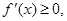
②当 时,
时,
③当 时,
时, 或
或 ,
, ;
;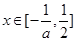 ,
,
综上,当 时,函数的单调递减区间为
时,函数的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,函数的单调递减区间为
时,函数的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;
当 时,函数的单调递减区间为
时,函数的单调递减区间为 单调递增区间为
单调递增区间为
……………………………………………………………………10分
(3)当 时,
时,
∵ ,∴
,∴ ∴
∴ ,
,
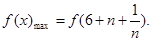 ………………………………………………12分
………………………………………………12分
由题意, 恒成立。
恒成立。
令 ,且
,且 在
在 上单调递增,
上单调递增,
 ,因此
,因此 ,而
,而 是正整数,故
是正整数,故 ,
,
所以, 时,存在
时,存在 ,
, 时,对所有
时,对所有 满足题意,∴
满足题意,∴
 ,没有极大值.
,没有极大值.(2)综上,当
 时,函数的单调递减区间为
时,函数的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;当
 时,函数的单调递减区间为
时,函数的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;当
 时,函数的单调递减区间为
时,函数的单调递减区间为 单调递增区间为
单调递增区间为
(3)
 解析:
解析:(1)先求出函数的定义域,再求出函数的导数,研究其单调性求出
其极值;(2)令
 =0,得
=0,得 ,
, 比较
比较 与
与 的大小得
的大小得 和
和 的
的 范围,就得到了函数的单调区间;
范围,就得到了函数的单调区间;(3)解本题的关键是要使在区间
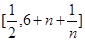 上总有
上总有 个数使得
个数使得 成立,只需
成立,只需 即可。
即可。解:(1)函数
 的定义域为
的定义域为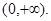 ……………………………………1分
……………………………………1分当
 时,
时, ,∴
,∴ ………………2分
………………2分由
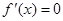 得
得
 随
随 变化如下表:
变化如下表: |  |  | 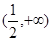 |
 | — | 0 | + |
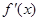 | ↘ | 极小值 | ↙ |
 ,没有极大值. …………………………4分
,没有极大值. …………………………4分(2)由题意,

令
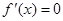 得
得 ,
, ………………………………………………6分
………………………………………………6分若
 ,由
,由 得
得 ;由
;由 得
得 …………7分
…………7分若
 ,①当
,①当 时,
时, ,
, 或
或 ,
, ;
;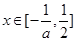 ,
,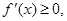
②当
 时,
时,
③当
 时,
时, 或
或 ,
, ;
;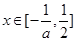 ,
,
综上,当
 时,函数的单调递减区间为
时,函数的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;当
 时,函数的单调递减区间为
时,函数的单调递减区间为 ,单调递增区间为
,单调递增区间为 ;
;当
 时,函数的单调递减区间为
时,函数的单调递减区间为 单调递增区间为
单调递增区间为
……………………………………………………………………10分
(3)当
 时,
时,
∵
 ,∴
,∴ ∴
∴ ,
,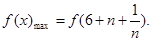 ………………………………………………12分
………………………………………………12分由题意,
 恒成立。
恒成立。令
 ,且
,且 在
在 上单调递增,
上单调递增, ,因此
,因此 ,而
,而 是正整数,故
是正整数,故 ,
,所以,
 时,存在
时,存在 ,
, 时,对所有
时,对所有 满足题意,∴
满足题意,∴

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 满足如下条件:当
满足如下条件:当 时,
时, ,且对任意
,且对任意 ,都有
,都有 .
. 处的切线方程;
处的切线方程; ,
, 时,函数
时,函数 ,
, ,使得等式
,使得等式
 (
(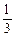 x3+bx2+cx+bc,
x3+bx2+cx+bc, ,试确定b、c的值;
,试确定b、c的值; x3+bx2+cx+bc,
x3+bx2+cx+bc, ,试确定b、c的值;
,试确定b、c的值;