题目内容
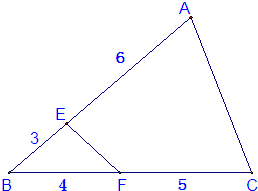 如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,那么三角形BEF面积和四边形AEFC面积的比是
如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,那么三角形BEF面积和四边形AEFC面积的比是4:23
4:23
.分析:连接AF,因为BE=3,AE=6,可得BE:AB=1:3,所以根据高一定时,三角形的面积与底成正比例的性质可得:三角形BEF的面积=
三角形ABF的面积;同理,BE=4,FC=5,所以三角形ABF=
三角形ABC,由此即可得出三角形BEF的面积=
×
三角形ABC的面积=
三角形ABC的面积,即三角形BEF的面积:三角形ABC的面积=4:27,则三角形BEF:四边形AEFC=4:23.

| 1 |
| 3 |
| 4 |
| 9 |
| 1 |
| 3 |
| 4 |
| 9 |
| 4 |
| 27 |

解答:解:连接AF,因为BE=3,AE=6,则AB=9,
可得BE:AB=3:9=1:3,
所以三角形BEF的面积=
三角形ABF的面积;
同理,BE=4,FC=5,三角形ABF=
三角形ABC,
所以三角形BEF的面积=
×
三角形ABC的面积=
三角形ABC的面积,
即三角形BEF的面积:三角形ABC的面积=4:27,
则三角形BEF:四边形AEFC=4:23.
故答案为:4:23.
可得BE:AB=3:9=1:3,
所以三角形BEF的面积=
| 1 |
| 3 |
同理,BE=4,FC=5,三角形ABF=
| 4 |
| 9 |
所以三角形BEF的面积=
| 1 |
| 3 |
| 4 |
| 9 |
| 4 |
| 27 |
即三角形BEF的面积:三角形ABC的面积=4:27,
则三角形BEF:四边形AEFC=4:23.
故答案为:4:23.
点评:此题考查了高一定时,三角形的面积与底成正比例的性质的灵活应用.

练习册系列答案
相关题目
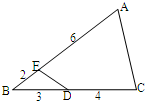 如图所示,三角形ABC被线段DE分成三角形BDE和四边形ACDE两部分,问:三角形BDE的面积是四边形ACDE面积的几分之几?
如图所示,三角形ABC被线段DE分成三角形BDE和四边形ACDE两部分,问:三角形BDE的面积是四边形ACDE面积的几分之几?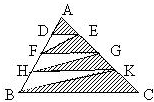 如图,三角形ABC的边AB,AC被分成四等份,已知三角形ADE的面积是10cm2,三角形中阴影部分的面积是
如图,三角形ABC的边AB,AC被分成四等份,已知三角形ADE的面积是10cm2,三角形中阴影部分的面积是 如图中的三角形ABC被分成了阴影、空白两部分,D是BC的中点,E是AB的三等分点,求阴影部分面积是空白部分面积的几分之几?
如图中的三角形ABC被分成了阴影、空白两部分,D是BC的中点,E是AB的三等分点,求阴影部分面积是空白部分面积的几分之几?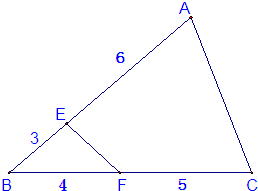 如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,那么三角形BEF面积和四边形AEFC面积的比是________.
如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,那么三角形BEF面积和四边形AEFC面积的比是________.