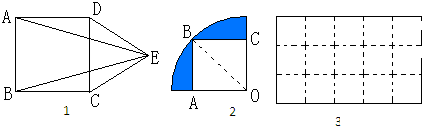题目内容
图形问题:
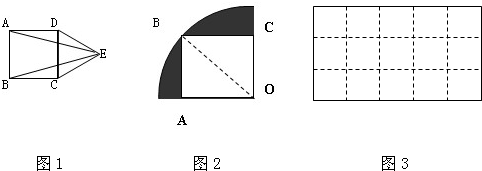
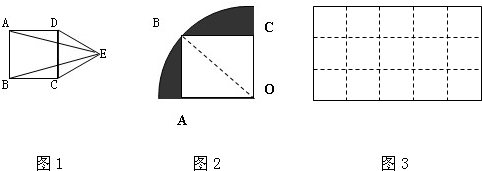
(1)如图1,ABCD是正方形,CDE是正三角形,那么∠AEB=______
(2)如图2所示,正方形ABCO在四分之一圆中,如果圆的半径是1厘米,则阴影部分的面积是多少平方厘米?
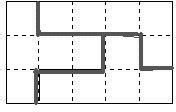
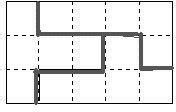
(3)图3是一张长方形的硬纸板,如果沿着图中虚线把这张硬纸板剪成三块,使每块都可以折成一个无盖的正方体.该怎样剪?(在图中画出来)
解:(1)正方形、正三角形各边长相等,故DA=DE,
所以∠DAE=∠DEA,
又因为∠ADE=90°+60°=150°,
所以∠DEA=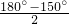 =15,
=15,
同理可证∠CEB=15°,
所以∠AEB=∠DEC-∠DEA-∠CEB=30°.
(2)3.14×12÷4-1×1÷2,
=0.785-0.5,
=0.285(平方厘米);
答:阴影部分的面积是0.285平方厘米.
(3)如图:
故答案为:30°.
分析:(1)正方形、正三角形各边长相等,故DA=DE,CB=CE,所以∠DAE=∠DEA,∠CBE=∠CEB,因为∠ADE=90°+60°=150°,所以∠DEA=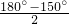 =15°,同理可证∠CEB=15°,即可求∠AEB的大小;
=15°,同理可证∠CEB=15°,即可求∠AEB的大小;
(2)先根据“圆的面积=πr2”求出圆的面积,进而求出圆面积的 ,然后减去正方形的面积,即可.
,然后减去正方形的面积,即可.
(3)
点评:(1)题考查了正方形各边长相等的性质,正三角形各内角为60°,等腰三角形的性质,本题中正确计算∠DEA和∠CEB是解题的关键.
(2)考查了正方形面积的计算和圆面积的计算方法;
(3)考查了正方体的表面展开图,最好动手操作一下便于理解.
所以∠DAE=∠DEA,
又因为∠ADE=90°+60°=150°,
所以∠DEA=
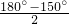 =15,
=15,同理可证∠CEB=15°,
所以∠AEB=∠DEC-∠DEA-∠CEB=30°.
(2)3.14×12÷4-1×1÷2,
=0.785-0.5,
=0.285(平方厘米);
答:阴影部分的面积是0.285平方厘米.
(3)如图:

故答案为:30°.
分析:(1)正方形、正三角形各边长相等,故DA=DE,CB=CE,所以∠DAE=∠DEA,∠CBE=∠CEB,因为∠ADE=90°+60°=150°,所以∠DEA=
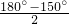 =15°,同理可证∠CEB=15°,即可求∠AEB的大小;
=15°,同理可证∠CEB=15°,即可求∠AEB的大小;(2)先根据“圆的面积=πr2”求出圆的面积,进而求出圆面积的
 ,然后减去正方形的面积,即可.
,然后减去正方形的面积,即可.(3)

点评:(1)题考查了正方形各边长相等的性质,正三角形各内角为60°,等腰三角形的性质,本题中正确计算∠DEA和∠CEB是解题的关键.
(2)考查了正方形面积的计算和圆面积的计算方法;
(3)考查了正方体的表面展开图,最好动手操作一下便于理解.

练习册系列答案
相关题目