题目内容
将 化为小数后,小数点后第2011位上的数字是
化为小数后,小数点后第2011位上的数字是
- A.4
- B.3
- C.2
- D.1
D
分析:首先根据分数化成小数的方法,用分子除以分母,把 化成小数,看它的循环节是几位数,根据“周期问题”,用2011除以它的循环节的位数,如果能整除,第2011上的数字就是循环节的末位上的数字,如果不能整除,余数是几就从循环节的首位起数出第几位,该位上的数字就是所求问题.
化成小数,看它的循环节是几位数,根据“周期问题”,用2011除以它的循环节的位数,如果能整除,第2011上的数字就是循环节的末位上的数字,如果不能整除,余数是几就从循环节的首位起数出第几位,该位上的数字就是所求问题.
解答: =0.
=0. 4285
4285 ,循环节是6位数;
,循环节是6位数;
2011÷6=335…1;余数是1也就是循环节首位上的数字1;
所以小数点后第2011位上的数字是1.
点评:此题主要考查分数化成小数的方法,以及根据“周期问题”判断循环小数的某一位上数字是几的方法.
分析:首先根据分数化成小数的方法,用分子除以分母,把
 化成小数,看它的循环节是几位数,根据“周期问题”,用2011除以它的循环节的位数,如果能整除,第2011上的数字就是循环节的末位上的数字,如果不能整除,余数是几就从循环节的首位起数出第几位,该位上的数字就是所求问题.
化成小数,看它的循环节是几位数,根据“周期问题”,用2011除以它的循环节的位数,如果能整除,第2011上的数字就是循环节的末位上的数字,如果不能整除,余数是几就从循环节的首位起数出第几位,该位上的数字就是所求问题.解答:
 =0.
=0. 4285
4285 ,循环节是6位数;
,循环节是6位数;2011÷6=335…1;余数是1也就是循环节首位上的数字1;
所以小数点后第2011位上的数字是1.
点评:此题主要考查分数化成小数的方法,以及根据“周期问题”判断循环小数的某一位上数字是几的方法.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
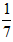 化为小数后,小数点后面第2008位上的数字是
化为小数后,小数点后面第2008位上的数字是