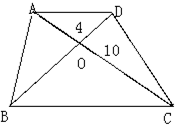
题目内容
9.(1)如图(1),在三角形ABC中,D为BC边上的中点,则三角形ABD和三角形ADC的面积相等,那么在图(2)中,如果M、N分别为四边形ABCD的边AD、BC的中点,则图中四边形BNDM的面积S1和四边形ABCD的面积S之间的关系是1:2;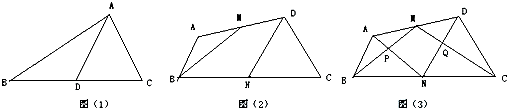
(2)如图(3),在四边形ABCD中,M、N分别为AD、BC的中点,MB交AN于P,MC交DN于Q,若四边形MPNQ的面积为36,求两个三角形ABP、DCQ的面积和.
分析 (1)连结BD,根据等底等高的三角形的面积相等,可知三角形BDM的面积等于三角形ABM的面积,三角形CDN的面积等于三角形BDN的面积,据此解答;
(2)如图:连结BD,根据等底等高的三角形的面积相等进行解答即可;
解答 解:(1)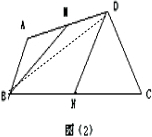
根据等底等高的三角形的面积相等,可知三角形BDM的面积等于三角形ABM的面积,三角形CDN的面积等于三角形BDN的面积,
可知S△BDM+S△BDN=△ABM+S△CDN
S四边形BNDM=△ABM+S△CDN
2S四边形BNDM=S四边形ABCD
S四边形BNDM:S四边形ABCD=1:2
答:图中四边形BNDM的面积S1和四边形ABCD的面积S之间的关系是 1:2.
(2)连结BD,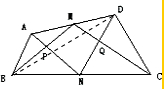
根据三角形面积公式S=$\frac{1}{2}$ah,
三角形ABN和MBN面积相等;三角形PBN面积为重叠面积;
三角形MCN和DCN面积相等;三角形QCN面积为重叠面积;
可得:A三角形BP+DCQ面积和等于三角形MPN+MQN,等于36.
答:两个三角形ABP、DCQ的面积和是36.
点评 解答本题的关键是等底等高的三角形的面积相等.

练习册系列答案
相关题目
17.一张边长为a米的正方形,如果在这张纸上剪4个相等且最大的圆,四个圆的面积和约是这张纸的( )
| A. | 78.5% | B. | 80% | C. | 75% | D. | 82% |