题目内容
4．一个圆柱和一个圆锥，它们的底面半径比是2：3，体积之比是2：5，它们的高的比是多少？分析 根据“一个圆柱和一个圆锥的底面半径之比是2：3，体积之比是2：5，”把圆柱的底面半径看作2份，圆锥的底面半径是3份，圆柱的体积是2份，圆锥的体积是5份；再根据圆柱与圆锥的体积公式，分别得出圆柱与圆锥的高的求法，进而得出答案．
解答 解：因为，V=πr2h
所以，h=V÷（πr2）
=2÷（4π）
=$\frac{π}{2}$
因为V=$\frac{1}{3}$πr2h
所以h=3V÷（πr2）
=5×3÷（9π）
=$\frac{5π}{3}$
所以圆柱的高与圆锥的高的比是：$\frac{π}{2}$：$\frac{5π}{3}$=3：10
答：它们的高的比是3：10．
点评 由于是求两个数的比，所以把对应的量看作份数，另外在计算时π不用代入数据．
练习册系列答案
相关题目
13．
| 脱式算得数．（能简算的要简算） 13.6-（2.6+0.25÷25%） | 56×（$\frac{3}{7}$-$\frac{3}{8}$） |
| 12.5×2.5×32 | （$\frac{3}{4}$-$\frac{2}{3}$）÷$\frac{5}{6}$ |
| $\frac{4}{25}$×33+$\frac{4}{25}$×67 | $\frac{3}{4}$×4÷4×$\frac{3}{4}$． |
用正数或负数表示．
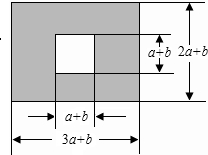如图，某市有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修一座雕像，则绿化的面积是多少平方米？并求出当a=3，b=2时绿化的面积．