题目内容
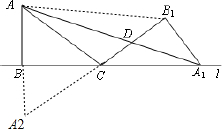
 图中,直角三角形ABC 的两条直角边AB 和BC 的长度分别为3和4,将三角形ABC绕点C顺时针旋转至A1B1C,使得A1C与B1C在直线l上.
图中,直角三角形ABC 的两条直角边AB 和BC 的长度分别为3和4,将三角形ABC绕点C顺时针旋转至A1B1C,使得A1C与B1C在直线l上.A1A交B1C于D,求
| AD | A1D |
分析:如图,作三角形ABC关于A1B对称的三角形A2BC,连结AB1,A2B和A2C,根据角之间的关系推出A2、C、B1 三点共线,然后根据三角形的面积与底成正比的关系,解决问题.
解答:解:如图,作三角形ABC关于A1B对称的三角形A2BC,连结AB1,A2B和A2C,
因为AB=3,BC=4,所以A2C=5,B1C=4,S△AA2C=2S△ABC=12.
因为∠ACB+∠ACB1+∠A1CB1=∠ACB+∠ACB1+∠A2CB=180°,
所以A2、C、B1 三点共线,且
=
=
,即S△AB1C=
.
因为
=
,且
=
,
所以
=
.
因此,
=
×
=
.

因为AB=3,BC=4,所以A2C=5,B1C=4,S△AA2C=2S△ABC=12.
因为∠ACB+∠ACB1+∠A1CB1=∠ACB+∠ACB1+∠A2CB=180°,
所以A2、C、B1 三点共线,且
| S△AA2C |
| S△AB1C |
| A2C |
| B1C |
| 5 |
| 4 |
| 48 |
| 5 |
因为
| S△ACD |
| S△CDA1 |
| AD |
| A1D |
| S△ADB1 |
| S△B1A1D |
| AD |
| A1D |
所以
| S△ACD+S△AB1D |
| S△CDA+S△CA1D |
| AD |
| A1D |
因此,
| AD |
| A1D |
| 48 |
| 5 |
| 1 |
| 6 |
| 8 |
| 5 |
点评:此题通过作辅助线,运用三角形的面积与底成正比的关系,解决问题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 如图,等腰直角三角形ABC中,AB=AC=2,D在BC的延长线上且BC=CD,E为AB上一点,ED交AC于P,EC与AD平行,求三角形BEC的面积.
如图,等腰直角三角形ABC中,AB=AC=2,D在BC的延长线上且BC=CD,E为AB上一点,ED交AC于P,EC与AD平行,求三角形BEC的面积. 如图,在直角三角形ABC中,AB=4cm,AC=3cm,BC=5cm?
如图,在直角三角形ABC中,AB=4cm,AC=3cm,BC=5cm? (2011?长春模拟)如图,在直角三角形ABC中,四边形EFBH是正方形,AB=21厘米,BC=28厘米,AC=35厘米,ED垂直于AC,ED=8.4厘米,正方形EFBH的面积是多少厘米?
(2011?长春模拟)如图,在直角三角形ABC中,四边形EFBH是正方形,AB=21厘米,BC=28厘米,AC=35厘米,ED垂直于AC,ED=8.4厘米,正方形EFBH的面积是多少厘米?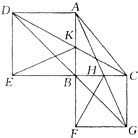 如图,ABC是一个直角三角形,AB≠CB,ABED和BCGF是正方形.AG、BC交于H,DC,AB交于K.那么在此图中,与三角形ABC面积相等的三角形(不包括三角形ABC)的个数是( )
如图,ABC是一个直角三角形,AB≠CB,ABED和BCGF是正方形.AG、BC交于H,DC,AB交于K.那么在此图中,与三角形ABC面积相等的三角形(不包括三角形ABC)的个数是( )