题目内容
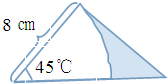
 如图,等腰直角三角形ABC中,AB=AC=2,D在BC的延长线上且BC=CD,E为AB上一点,ED交AC于P,EC与AD平行,求三角形BEC的面积.
如图,等腰直角三角形ABC中,AB=AC=2,D在BC的延长线上且BC=CD,E为AB上一点,ED交AC于P,EC与AD平行,求三角形BEC的面积.分析:根据题干可知EC∥AD,且BC=CD,根据平行线分线段成比例的性质,可得AE=EB,根据三角形的高一定时,三角形的面积与底成正比例的性质可得三角形BEC的面积=三角形ABC的面积的
,等腰直角三角形ABC的面积是2×2÷2=2,由此即可解答.
| 1 |
| 2 |
解答:解:因为EC∥AD,且BC=CD,可得AE=EB,
所以三角形BEC的面积=三角形ABC的面积的
,
因为等腰直角三角形ABC的面积是2×2÷2=2,
所以三角形BEC的面积是2×
=1,
答:三角形BEC的面积是1.
所以三角形BEC的面积=三角形ABC的面积的
| 1 |
| 2 |
因为等腰直角三角形ABC的面积是2×2÷2=2,
所以三角形BEC的面积是2×
| 1 |
| 2 |
答:三角形BEC的面积是1.
点评:此题考查了三角形的高一定时,三角形的面积与底成正比例的性质和平行线分线段成比例性质的综合应用.

练习册系列答案
相关题目
 如图,等腰直角三角形ABC中,AC=BC,计算阴影部分的面积.
如图,等腰直角三角形ABC中,AC=BC,计算阴影部分的面积.
 如图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等.求扇形所在的圆面积.
如图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等.求扇形所在的圆面积.