题目内容
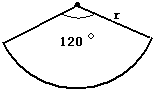如图扇形的圆心角是120°，半径是r．请你想像，用这个扇形围成一个高为h的圆锥（接缝处不计），圆锥的高h与扇形的半径r之间的关系是
- A.h＞r
- B.h=r
- C.h＜r
C
分析：把该扇形围成圆锥后，扇形的半径即围成后圆锥的母线，圆锥的高与底面半径、圆锥母线构成直角三角形的三边，根据三角形中，斜边最长，所以扇形的高小于圆锥的母线（即扇形的半径r）；据此判断即可．
解答：由分析知：用这个扇形围成一个高为h的圆锥（接缝处不计），圆锥的高h与扇形的半径r之间的关系：h＜r；
故选：C．
点评：解答此题应明确：圆锥的侧面展开图是一个扇形，此扇形的半径等于圆锥的母线长，圆锥的高与底面半径、圆锥母线构成直角三角形的三边．
分析：把该扇形围成圆锥后，扇形的半径即围成后圆锥的母线，圆锥的高与底面半径、圆锥母线构成直角三角形的三边，根据三角形中，斜边最长，所以扇形的高小于圆锥的母线（即扇形的半径r）；据此判断即可．
解答：由分析知：用这个扇形围成一个高为h的圆锥（接缝处不计），圆锥的高h与扇形的半径r之间的关系：h＜r；
故选：C．
点评：解答此题应明确：圆锥的侧面展开图是一个扇形，此扇形的半径等于圆锥的母线长，圆锥的高与底面半径、圆锥母线构成直角三角形的三边．
练习册系列答案
相关题目
（2012?武汉模拟）如图，在圆心角为直角的扇形OAB中，分别以OA、OB为直径作两个半圆，在扇形OAB内随机取一点，则此点取阴影部分的可能性是
在一次对某小区500户家庭拥有电视机的数量的调查中，调查结果如下图所示，根据图中所给信息回答问题：
如图，是一个扇形统计图，那么从图中可以得出的正确结论的个数是（ ）
在一次对某小区500户家庭拥有电视机的数量的调查中，调查结果如下图所示，根据图中所给信息回答问题：
，那么拥有2台电视机的家庭有几户？
如图，是一个扇形统计图，那么从图中可以得出的正确结论的个数是