题目内容
 三角形ABC的面积是80平方厘米,EC=AE,BD=4AD,三角形ADE的面积是_______平方厘米.
三角形ABC的面积是80平方厘米,EC=AE,BD=4AD,三角形ADE的面积是_______平方厘米.
- A.5
- B.8
- C.10
- D.20
B
分析:连接CD,根据等高的三角形面积比等于底边比,由已知条件BD=4AD,可求△ADC与△ABC的面积之间的关系;同理由已知条件EC=AE,可求△ADE与△ADC的面积之间的关系,从而求解.
解答:连接CD,

因为BD=4AD,即AB=5AD,
所以△ADC的面积=80÷5=16(平方厘米),
因为EC=AE,即AC=2AE,
所以△ADE的面积=16÷2=8(平方厘米).
答:三角形ADE的面积是8平方厘米.
故选:B.
点评:考查了灵活求解三角形的面积,关键是理解和掌握等高的三角形面积比等于底边比的运用.
分析:连接CD,根据等高的三角形面积比等于底边比,由已知条件BD=4AD,可求△ADC与△ABC的面积之间的关系;同理由已知条件EC=AE,可求△ADE与△ADC的面积之间的关系,从而求解.
解答:连接CD,

因为BD=4AD,即AB=5AD,
所以△ADC的面积=80÷5=16(平方厘米),
因为EC=AE,即AC=2AE,
所以△ADE的面积=16÷2=8(平方厘米).
答:三角形ADE的面积是8平方厘米.
故选:B.
点评:考查了灵活求解三角形的面积,关键是理解和掌握等高的三角形面积比等于底边比的运用.

练习册系列答案
相关题目
 如图,三角形ABC的面积是16,D是AC的中点,E是BD的中点,那四边形CDEF的面积是多少?
如图,三角形ABC的面积是16,D是AC的中点,E是BD的中点,那四边形CDEF的面积是多少?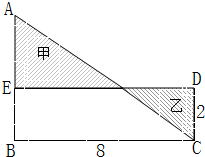 图中,阴影部分甲的面积比乙大4平方厘米.求三角形ABC的面积是
图中,阴影部分甲的面积比乙大4平方厘米.求三角形ABC的面积是
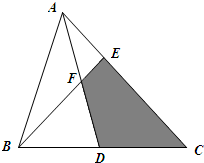 如图,在三角形ABC中,CE=2AE,F是AD的中点,三角形ABC的面积是1,那么阴影部分的面积是多少?
如图,在三角形ABC中,CE=2AE,F是AD的中点,三角形ABC的面积是1,那么阴影部分的面积是多少?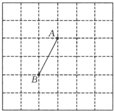 在6×6的方格中,每个小方格的边长是l厘米,A、B两点都在小方格的顶点上.现在要在小方格的顶点上找到一点C,连接AC和BC后,使三角形ABC的面积是2平方厘米.符合条件的C点最多有
在6×6的方格中,每个小方格的边长是l厘米,A、B两点都在小方格的顶点上.现在要在小方格的顶点上找到一点C,连接AC和BC后,使三角形ABC的面积是2平方厘米.符合条件的C点最多有