题目内容
在1、2、3…1997这1997个自然数中,最多能取________个数,使得在所取的这些数中任意两数之和都能被50整除.
39
分析:所取的这些数中任意两个之和能被50整除,则这些数本身都能被50整除,要最多的取出且使取出的任意两数被50整除,则必然是50,100,150,200,…
解答:根据题干分析可得:取出的这些数应是50的倍数:50、100、150、200…
假设所给自然数到2000,当50n=2000时,n=40,
此时最多可取40个数
现在所给数到1997,所以最多可取39个.
点评:所取的这些数中任意两个之和能被50整除,得出所取的数都应是50的倍数.
分析:所取的这些数中任意两个之和能被50整除,则这些数本身都能被50整除,要最多的取出且使取出的任意两数被50整除,则必然是50,100,150,200,…
解答:根据题干分析可得:取出的这些数应是50的倍数:50、100、150、200…
假设所给自然数到2000,当50n=2000时,n=40,
此时最多可取40个数
现在所给数到1997,所以最多可取39个.
点评:所取的这些数中任意两个之和能被50整除,得出所取的数都应是50的倍数.

练习册系列答案
相关题目

 :x=2
:x=2 :1.8
:1.8 ]×(1÷
]×(1÷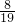 -2.375)]+2.901
-2.375)]+2.901 和原二班的
和原二班的