题目内容
18.只列式,不计算.挖一条水渠,王大伯每天挖这条水渠的$\frac{1}{12}$,李大伯每天挖这条水渠的$\frac{1}{15}$.(1)两人合作,每天挖这条水渠的几分之几?算式是:$\frac{1}{12}$+$\frac{1}{15}$
(2)两人合作,完成这条水渠的$\frac{2}{3}$,需要几天?算式是:$\frac{2}{3}$÷($\frac{1}{12}$+$\frac{1}{15}$)
(3)两人合作,几天能挖完这条水渠?算式是:1÷($\frac{1}{12}$+$\frac{1}{15}$)
(4)李大伯先挖5天,王大伯单独挖还要儿天?算式是:(1-$\frac{1}{15}$×5)÷$\frac{1}{12}$.
分析 (1)把两人的工作效率相加即可;
(2)(3)运用关系式:工作量÷工作效率=工作时间,列式解答;
(4)把这条水渠的长度看作单位“1”,先求出李大伯先挖5天的工作量,即$\frac{1}{15}$×5,然后用工作总量减去李大伯先挖5天的工作量,得出剩余工作量,再用剩余工作量除以王大伯的工作效率,解决问题.
解答 解:(1)$\frac{1}{12}$+$\frac{1}{15}$=$\frac{3}{20}$
答:两人合作,每天挖这条水渠的$\frac{3}{20}$.
(2)$\frac{2}{3}$÷($\frac{1}{12}$+$\frac{1}{15}$)
=$\frac{2}{3}$÷$\frac{3}{20}$
=$\frac{2}{3}$×$\frac{20}{3}$
=$\frac{40}{9}$(天)
答:需要几$\frac{40}{9}$.
(3)1÷($\frac{1}{12}$+$\frac{1}{15}$)
=1÷$\frac{3}{20}$
=$\frac{20}{3}$(天)
答:两人合作,$\frac{20}{3}$天能挖完这条水渠.
(4)(1-$\frac{1}{15}$×5)÷$\frac{1}{12}$
=$\frac{2}{3}$×12
=8(天)
答:王大伯单独挖还要8天.
故答案为:$\frac{1}{12}$+$\frac{1}{15}$,$\frac{2}{3}$÷($\frac{1}{12}$+$\frac{1}{15}$),1÷($\frac{1}{12}$+$\frac{1}{15}$),(1-$\frac{1}{15}$×5)÷$\frac{1}{12}$.
点评 此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
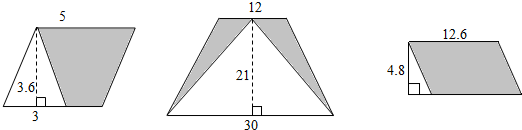
小学生10分钟应用题系列答案| A. | 16 | B. | 20 | C. | 24 | D. | 16或20 |
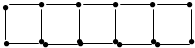 用一些长短相同的火柴棒按如图所示的方法连续摆放正方形,如果有208根火柴棒,那么可以连续摆放69个正方形.
用一些长短相同的火柴棒按如图所示的方法连续摆放正方形,如果有208根火柴棒,那么可以连续摆放69个正方形.