题目内容
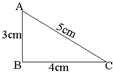 将直角三角形ABC分别以三条边为轴旋转一周,计算旋转后那个物体的体积.
将直角三角形ABC分别以三条边为轴旋转一周,计算旋转后那个物体的体积.(1)以AB为轴旋转
(2)以BC为轴旋转
(3)以AC为轴旋转.
分析:(1)根据直角三角形的特征,以它的一条直角边AB为轴旋转一周得到一个以旋转边为高,另一直角边为底面半径的圆锥;根据圆锥的体积公式V=
πr2h即可求出它的体积;
(2)根据直角三角形的特征,以它的一条直角边BC为轴旋转一周得到一个以旋转边为高,另一直角边为底面半径的圆锥;根据圆锥的体积公式V=
πr2h即可求出它的体积;
(3)根据直角三角形的特征,以它的一条斜边AC为轴旋转一周得到一个以旋转边为高,斜边上的高为底面半径的圆锥;根据圆锥的体积公式V=
πr2h即可求出它的体积.
| 1 |
| 3 |
(2)根据直角三角形的特征,以它的一条直角边BC为轴旋转一周得到一个以旋转边为高,另一直角边为底面半径的圆锥;根据圆锥的体积公式V=
| 1 |
| 3 |
(3)根据直角三角形的特征,以它的一条斜边AC为轴旋转一周得到一个以旋转边为高,斜边上的高为底面半径的圆锥;根据圆锥的体积公式V=
| 1 |
| 3 |
解答:解:(1)
×3.14×42×3,
=3.14×16,
=50.24(cm3).
答:以AB为轴旋转,旋转后那个物体的体积是50.24cm3.
(2)
×3.14×32×4,
=3.14×12,
=37.68(cm3).
答:以BC为轴旋转,旋转后那个物体的体积是37.68cm3.
(3)3×4÷5=2.4(cm),
×3.14×2.42×5,
=3.14×9.6,
=30.144(cm3).
答:以AC为轴旋转,旋转后那个物体的体积是30.144cm3.
| 1 |
| 3 |
=3.14×16,
=50.24(cm3).
答:以AB为轴旋转,旋转后那个物体的体积是50.24cm3.
(2)
| 1 |
| 3 |
=3.14×12,
=37.68(cm3).
答:以BC为轴旋转,旋转后那个物体的体积是37.68cm3.
(3)3×4÷5=2.4(cm),
| 1 |
| 3 |
=3.14×9.6,
=30.144(cm3).
答:以AC为轴旋转,旋转后那个物体的体积是30.144cm3.
点评:本题考查了图形的旋转,解答此题的关键是:能够想象出所得的立体图形的形状和特征,能灵活运用圆锥的体积计算公式进行解答.

练习册系列答案
相关题目
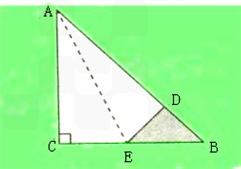
 (2011?郑州模拟)直角三角形ABC的三条边分别是5cm,3cm和4cm,将它的直角边AC对折到斜边AB上,使AC 与AD重合,如图,则图中阴影部分(未重叠部分)的面积是多少cm2?
(2011?郑州模拟)直角三角形ABC的三条边分别是5cm,3cm和4cm,将它的直角边AC对折到斜边AB上,使AC 与AD重合,如图,则图中阴影部分(未重叠部分)的面积是多少cm2? 直角三角形ABC的三条边分别是5厘米、3厘米、4厘米,将它的直角边AC对折到斜边AB上,使AC与AD重合,如图,则阴影部分的面积是
直角三角形ABC的三条边分别是5厘米、3厘米、4厘米,将它的直角边AC对折到斜边AB上,使AC与AD重合,如图,则阴影部分的面积是 直角三角形ABC的三条边分别是5cm,3cm和4cm,将它的直角边AC对折到斜边AB上,使AC 与AD重合,如图,则图中阴影部分(未重叠部分)的面积是多少cm2?
直角三角形ABC的三条边分别是5cm,3cm和4cm,将它的直角边AC对折到斜边AB上,使AC 与AD重合,如图,则图中阴影部分(未重叠部分)的面积是多少cm2?