题目内容
一个正方体削成一个最大的圆锥,削去部分占正方体体积的________%.
73.8
分析:设正方体的棱长是1,则圆锥的底面直径和高都是1,由此利用正方体和圆锥的体积公式分别求出它们的体积,从而即可计算出削去部分的体积,再利用除法计算即可求出削去部分占正方体的体积的百分之几.
解答:设正方体的棱长是1,则圆锥的底面直径和高都是1,
则正方体的体积是:1×1×1=1;
圆锥的体积是: ×3.14×
×3.14× ×1=
×1= ×3.14×
×3.14× =
=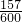 ,
,
则削去部分的体积是:1-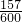 =
=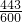 ,
,
所以削去部分占正方体体积的: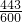 ÷1×100%≈73.8%,
÷1×100%≈73.8%,
答:削去部分占正方体体积的73.8%.
故答案为:73.8.
点评:抓住一个正方体削成一个最大的圆锥,则圆锥的底面直径和高与正方体的棱长相等,是解决此类问题的关键.
分析:设正方体的棱长是1,则圆锥的底面直径和高都是1,由此利用正方体和圆锥的体积公式分别求出它们的体积,从而即可计算出削去部分的体积,再利用除法计算即可求出削去部分占正方体的体积的百分之几.
解答:设正方体的棱长是1,则圆锥的底面直径和高都是1,
则正方体的体积是:1×1×1=1;
圆锥的体积是:
 ×3.14×
×3.14× ×1=
×1= ×3.14×
×3.14× =
=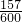 ,
,则削去部分的体积是:1-
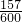 =
=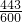 ,
,所以削去部分占正方体体积的:
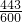 ÷1×100%≈73.8%,
÷1×100%≈73.8%,答:削去部分占正方体体积的73.8%.
故答案为:73.8.
点评:抓住一个正方体削成一个最大的圆锥,则圆锥的底面直径和高与正方体的棱长相等,是解决此类问题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目