题目内容
 如图中,四边形ABCD的对角线AC与BD相交于O,E为BC的中点,三角形ABO的面积为45,三角形ADO的面积为18,三角形CDO的面积为69.则三角形AED的面积等于
如图中,四边形ABCD的对角线AC与BD相交于O,E为BC的中点,三角形ABO的面积为45,三角形ADO的面积为18,三角形CDO的面积为69.则三角形AED的面积等于分析:若将AD作为底边,因为点E为BC的中点,那么△ADB,△ADE,△ADC的高为等差数列(可以认为中间三角形的高是两边三角形的高的平均数),所以面积也呈等差数列(可以认为中间三角形的面积是两边三角形的面积的平均数).据此可解.
解答:解:若将AD作为底边,因为点E为BC的中点,
所以△ADE的高为△ADB和△ADC的高的平均数,
因此△ADE的面积就等于△ADB和△ADC的面积的平均数.
所以,S△ADE=(S△ADB+S△ADC)÷2
=(45+18+18+69)÷2
=75;
答:三角形AED的面积等于75.
所以△ADE的高为△ADB和△ADC的高的平均数,
因此△ADE的面积就等于△ADB和△ADC的面积的平均数.
所以,S△ADE=(S△ADB+S△ADC)÷2
=(45+18+18+69)÷2
=75;
答:三角形AED的面积等于75.
点评:本题难度较大,解决的关键是理解以AD为底的三个三角形的面积之间的关系.

练习册系列答案
相关题目
 (2010?常熟市模拟)如图,在三角形ABC中,D为BC的中点,E为AB上的一点,且BE=
(2010?常熟市模拟)如图,在三角形ABC中,D为BC的中点,E为AB上的一点,且BE=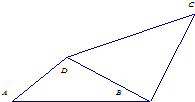 如图,在四边形ABCD中,∠ABC=∠ADB=105°,∠CDB=60°,∠CBD=75°,AB=CD=15厘米,四边形ABCD的面积是
如图,在四边形ABCD中,∠ABC=∠ADB=105°,∠CDB=60°,∠CBD=75°,AB=CD=15厘米,四边形ABCD的面积是