Question

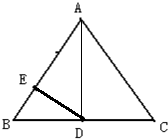
（2010?常熟市模拟）如图，在三角形ABC中，D为BC的中点，E为AB上的一点，且BE=

1

3

AB，已知四边形ACDE的面积是35，求三角形ABC的面积．

Answer 1

分析：如图，连接DE，AD，因为BE=

1

3

AB，所以△BDE的面积=

1

3

△ABD的面积，又因为D为BC的中点，所以△ABD的面积=△ACD的面积，所以△BDE的面积=

1

6

△ABC的面积，故四边形ACDE的面积=

5

6

△ABC的面积，由此即可解决问题．

解答：解：连接DE、AD根据题干分析可得：
因为BE=

1

3

AB，所以△BDE的面积=

1

3

△ABD的面积；
又因为D为BC的中点，所以△ABD的面积=△ACD的面积，所以△BDE的面积=

1

6

△ABC的面积，
故四边形ACDE的面积=

5

6

△ABC的面积，
所以△ABC的面积是：35÷

5

6

=42，
答：三角形ABC的面积是42．

点评：此题考查了利用了高一定时，三角形的面积与底成正比的关系灵活应用，