Question

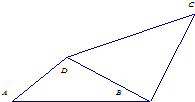如图，在四边形ABCD中，∠ABC=∠ADB=105°，∠CDB=60°，∠CBD=75°，AB=CD=15厘米，四边形ABCD的面积是

112.5平方厘米

．

Answer 1

分析：将三角形DBC平移，AB和CD边重合，形成AB'BD四边形，因为∠ABC=∠ADB=105°，∠CBD=75°，所以∠DBA=105°-75°=30°，∠DAB=180°-105°-30°=45°，∠CDB=60°，即∠BAB′=60°，所以∠DAB′=105°，而∠CBD=75°，即∠BB′A=75°，所以四边形AB′BD是等腰梯形；由三角形AB′B和三角形DBB′全等，得出∠B′DB=60°，∠DB′B=45°，所以AB⊥B′D，再根据对角线互相垂直的对角线互相垂直的对角线互相垂直的梯形的面积是两条对角线的乘积的一半，列式解答即可．

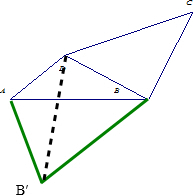
解答：解：因为∠ABC=∠ADB=105°，∠CBD=75°，所以∠DBA=105°-75°=30°，∠DAB=180°-105°-30°=45°，
因为∠CDB=60°，即∠BAB′=60°，
所以∠DAB′=45°+60°=105°，而∠CBD=75°，即∠BB′A=75°，
所以四边形AB′BD是等腰梯形；
因为三角形AB′B和三角形DBB′全等，
所以∠B′DB=60°，∠DB′B=45°，
所以AB⊥B′D，AB=B′D，
面积为：15×15÷2=112.5（平方厘米），
答：四边形ABCD的面积是112.5平方厘米．
故答案为：112.5平方厘米．

点评：本题主要是利用平移的方法，将两个三角形组成一个等腰梯形，再利用互相垂直的对角线的乘积的一半是此等腰梯形的面积解决问题．