题目内容
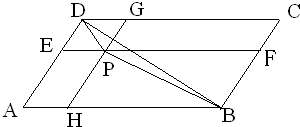 如图,P为平行四边形ABCD内一点,过P分别做AB,AD的平行线.交平行四边形各边分别于E、F、G、H.若平行四边形AHPE的面积为4,平行四边形PFCG的面积为7.求三角形PBD的面积.
如图,P为平行四边形ABCD内一点,过P分别做AB,AD的平行线.交平行四边形各边分别于E、F、G、H.若平行四边形AHPE的面积为4,平行四边形PFCG的面积为7.求三角形PBD的面积.分析:由题意可得EPGD、GPFC、EPHA、PHBF均为平行四边形,进而通过三角形与四边形之间的面积转化,最终不难得出结论.
解答:解:显然EPGD、GPFC、EPHA、PHBF均为平行四边形,
所以S△DEP=S△DGP=
×S平行四边形DEPG,
所以S△PHBS△PHB=S△PBF=
S平行四边形PHBF,
又因为S△ADB=S△EPD+S平行四边形AHPE+S△PHB+S△PDB①,
S△BCD=S△PDG+S平行四边形PFCG+S△PFB-S△PDB②,
①-②得0=S平行四边形AHPE-S平行四边形PFCG+2S△PDB,
即2S△PDB=7-4=3
S△PDB=1.5.
答:三角形PBD的面积是1.5.
所以S△DEP=S△DGP=
| 1 |
| 2 |
所以S△PHBS△PHB=S△PBF=
| 1 |
| 2 |
又因为S△ADB=S△EPD+S平行四边形AHPE+S△PHB+S△PDB①,
S△BCD=S△PDG+S平行四边形PFCG+S△PFB-S△PDB②,
①-②得0=S平行四边形AHPE-S平行四边形PFCG+2S△PDB,
即2S△PDB=7-4=3
S△PDB=1.5.
答:三角形PBD的面积是1.5.
点评:本题主要考查平行四边形的性质及三角形面积的计算,能够通过面积之间的转化熟练求解解答本题的关键.

练习册系列答案
相关题目
 如图,P为平行四边形ABCD外一点,已知三角形PAB与三角形PCD的面积分别为7平方厘米和3平方厘米,那么平行四边形ABCD的面积为
如图,P为平行四边形ABCD外一点,已知三角形PAB与三角形PCD的面积分别为7平方厘米和3平方厘米,那么平行四边形ABCD的面积为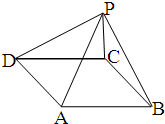 如图,P为平行四边形ABCD外一点,已知△PAB的面积为7cm2,△PCD的面积为3平方厘米,平行四边形的面积是多少?
如图,P为平行四边形ABCD外一点,已知△PAB的面积为7cm2,△PCD的面积为3平方厘米,平行四边形的面积是多少? 如图,P为平行四边形ABCD内一点,过P分别做AB,AD的平行线.交平行四边形各边分别于E、F、G、H.若平行四边形AHPE的面积为4,平行四边形PFCG的面积为7.求三角形PBD的面积.
如图,P为平行四边形ABCD内一点,过P分别做AB,AD的平行线.交平行四边形各边分别于E、F、G、H.若平行四边形AHPE的面积为4,平行四边形PFCG的面积为7.求三角形PBD的面积. 如图,P为平行四边形ABCD外一点,已知△PAB的面积为7cm2,△PCD的面积为3平方厘米,平行四边形的面积是多少?
如图,P为平行四边形ABCD外一点,已知△PAB的面积为7cm2,△PCD的面积为3平方厘米,平行四边形的面积是多少?