题目内容
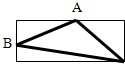 图中A、B是长方形长和宽的中点,长方形中间的三角形面积是长方形面积的( )%.
图中A、B是长方形长和宽的中点,长方形中间的三角形面积是长方形面积的( )%.分析:如图:设长方形的长为a,宽为b,因为“A、B是长方形长和宽的中点”,所以阴中间三角形的面积=长方形面积-三个直角三角形面积,代数计算出三角形面积,再除以长方形面积即可.
解答:解:设长方形的长为a,宽为b,
则三角形面积,
=ab-
ab÷2-
a×
b÷2-
ab÷2,
=
ab,
所以
ab÷ab=37.5%.
答:长方形中间的三角形面积是长方形面积的37.5%.
故选:B.
则三角形面积,
=ab-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 3 |
| 8 |
所以
| 3 |
| 8 |
答:长方形中间的三角形面积是长方形面积的37.5%.
故选:B.
点评:此题主要是先算出3个空白三角形的面积,用长方形的面积减空白部分的面积得阴影部分的面积,再与长方形的面积比.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
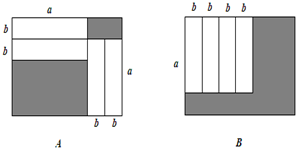 如图,A、B是两个大小完全一样的长方形,已知这两个长方形的长比宽长8厘米,图中的字母表示相应部分的长度.问:A、B 中阴影部分的周长哪个长?长多少?
如图,A、B是两个大小完全一样的长方形,已知这两个长方形的长比宽长8厘米,图中的字母表示相应部分的长度.问:A、B 中阴影部分的周长哪个长?长多少?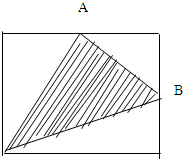 如图中A,B两点分别是长方形长和宽的中点,阴影部分的面积是36平方厘米,求长方形面积.
如图中A,B两点分别是长方形长和宽的中点,阴影部分的面积是36平方厘米,求长方形面积.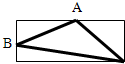 图中A、B是长方形长和宽的中点,长方形中间的三角形面积是长方形面积的_____%.
图中A、B是长方形长和宽的中点,长方形中间的三角形面积是长方形面积的_____%. 如图中A,B两点分别是长方形长和宽的中点,阴影部分的面积是36平方厘米,求长方形面积.
如图中A,B两点分别是长方形长和宽的中点,阴影部分的面积是36平方厘米,求长方形面积.