题目内容
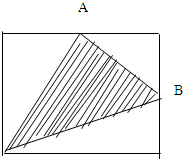 如图中A,B两点分别是长方形长和宽的中点,阴影部分的面积是36平方厘米,求长方形面积.
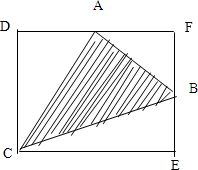
如图中A,B两点分别是长方形长和宽的中点,阴影部分的面积是36平方厘米,求长方形面积.分析:如图所示,设长方形的长和宽分别为a和b,则S△ADC=
a×b×
=
ab,S△AFB=
a×
b×
=
ab,S△BEC=
b×a×
=
ab,再据阴影部分的面积=长方形的面积-(S△ADC+S△AFB+S△BEC),据此即可求解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |

解答:解:设长方形的长和宽分别为a和b,
则S△ADC=
a×b×
=
ab,
S△AFB=
a×
b×
=
ab,
S△BEC=
b×a×
=
ab,
所以ab-(S△ADC+S△AFB+S△BEC)=36,
ab-(
ab+
ab+
ab)=36,
ab-
ab=36,
ab=36,
ab=96;
答:长方形的面积是96平方厘米.
则S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
S△AFB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
S△BEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
所以ab-(S△ADC+S△AFB+S△BEC)=36,
ab-(
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
ab-
| 5 |
| 8 |
| 3 |
| 8 |
ab=96;
答:长方形的面积是96平方厘米.
点评:解答此题的关键是分别用长方形的长和宽表示出空白三角形的面积,问题即可得解.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 (2009?和平区)如图是5×5的正方形网格图,设每个小方格的面积是1.A、B两点均在网格图中的交叉点上,A点的位置可用(2,3)表示,B点的位置可用(4,4)表示.现在要在网格图中的交叉点上找到C点,分别连接AB、BC、CA,使三角形ABC的面积为2.满足以上条件的C点在图上的不同位置分别用C1、C2、C3┅┅表示.如图所示,当C1的位置在(2,5)时,三解形ABC1的面积就是2.照样子,分别用C2、C3┅┅在右面网格图上以数对形式表示C点的其它所有可能位置.
(2009?和平区)如图是5×5的正方形网格图,设每个小方格的面积是1.A、B两点均在网格图中的交叉点上,A点的位置可用(2,3)表示,B点的位置可用(4,4)表示.现在要在网格图中的交叉点上找到C点,分别连接AB、BC、CA,使三角形ABC的面积为2.满足以上条件的C点在图上的不同位置分别用C1、C2、C3┅┅表示.如图所示,当C1的位置在(2,5)时,三解形ABC1的面积就是2.照样子,分别用C2、C3┅┅在右面网格图上以数对形式表示C点的其它所有可能位置.
 如图是5×5的正方形网格图,设每个小方格的面积是1.A、B两点均在网格图中的交叉点上,A点的位置可用(2,3)表示,B点的位置可用(4,4)表示.现在要在网格图中的交叉点上找到C点,分别连接AB、BC、CA,使三角形ABC的面积为2.满足以上条件的C点在图上的不同位置分别用C1、C2、C3┅┅表示.如图所示,当C1的位置在(2,5)时,三解形ABC1的面积就是2.照样子,分别用C2、C3┅┅在右面网格图上以数对形式表示C点的其它所有可能位置.
如图是5×5的正方形网格图,设每个小方格的面积是1.A、B两点均在网格图中的交叉点上,A点的位置可用(2,3)表示,B点的位置可用(4,4)表示.现在要在网格图中的交叉点上找到C点,分别连接AB、BC、CA,使三角形ABC的面积为2.满足以上条件的C点在图上的不同位置分别用C1、C2、C3┅┅表示.如图所示,当C1的位置在(2,5)时,三解形ABC1的面积就是2.照样子,分别用C2、C3┅┅在右面网格图上以数对形式表示C点的其它所有可能位置.