题目内容
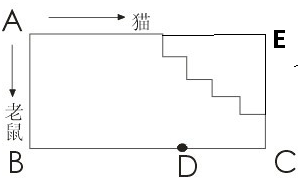
 (2013?广东模拟)如图为一阶梯的纵横面,一只老鼠沿长方形的两边A→B→D的路线逃跑,一只猫同时沿阶梯(折线)A→C→D的线路去追,结果在距离C点0.6米的D处,猫捉住老鼠,已知猫的速度是老鼠的
(2013?广东模拟)如图为一阶梯的纵横面,一只老鼠沿长方形的两边A→B→D的路线逃跑,一只猫同时沿阶梯(折线)A→C→D的线路去追,结果在距离C点0.6米的D处,猫捉住老鼠,已知猫的速度是老鼠的| 8 | 3 |
1.32米
1.32米
.分析:把楼梯的各条线段进行平移,可得到一个长方形ABCE;可得AB+BC=楼梯A→C的总长(即这个长方形周长的一半);猫捉鼠的路程之和为楼梯A→C的总长+线段CD长;老鼠逃窜的路程为AB+BC-线段CD长;根据时间一定时,所行走的路程与速度成正比的性质即可解决问题.

解答:解:把楼梯的各条线段进行平移,可得AB+BC=楼梯A→C的总长;
设A→C的路程为x米,则猫行走的路程为x+0.6米,老鼠行走的路程为x-0.6米,
因为猫和老鼠行走的时间相同,且猫的速度是老鼠的
,
根据时间一定时,路程与速度成正比的性质可得:
=
,根据比例的基本性质可得:
3(x+0.6)=8(x-0.6),
3x+1.8=8x-4.8,
5x=6.6,
x=1.32,
答:A→C的路程为1.32米.
故答案为:1.32米.
设A→C的路程为x米,则猫行走的路程为x+0.6米,老鼠行走的路程为x-0.6米,
因为猫和老鼠行走的时间相同,且猫的速度是老鼠的
| 8 |
| 3 |
根据时间一定时,路程与速度成正比的性质可得:
| x+0.6 |
| x-0.6 |
| 8 |
| 3 |
3(x+0.6)=8(x-0.6),
3x+1.8=8x-4.8,
5x=6.6,
x=1.32,
答:A→C的路程为1.32米.
故答案为:1.32米.
点评:本题主要考查时间一定时,路程与速度成正比的性质的灵活应用,这里关键是得到楼梯的长度等于AB与BC之和,从而得出猫和老鼠各自行走的路程.

练习册系列答案
相关题目
 (2013?广东模拟)如图中每一个图形都是由一些小△组成的,从第一个图形开始,小△的个数分别是1,4,9…,那么第八个图形的小△个数.共有
(2013?广东模拟)如图中每一个图形都是由一些小△组成的,从第一个图形开始,小△的个数分别是1,4,9…,那么第八个图形的小△个数.共有