题目内容
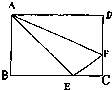 如图在长方形ABCD中,△ABE、△ADF、四边形AECF的面积相等.△AEF的面积是长方形ABCD面积的
如图在长方形ABCD中,△ABE、△ADF、四边形AECF的面积相等.△AEF的面积是长方形ABCD面积的分析:由题意可知:△ABE、△ADF、四边形AECF的面积都等于长方形的面积的
,据此再用长方形的长和宽表示出三角形FCE的面积,依据减法和除法的意义即可求解.
| 1 |
| 3 |
解答:解:假设长方形的长和宽分别为a和b,
则长方形的面积为:ab,
△ABE、△ADF、四边形AECF的面积都等于
ab,
则BE为:
ab×2÷b=
a,所以CE为:
a,
同理,DF为:
ab×2÷a=
b,所以CF为:
b,
因此三角形FCE的面积为
a×
b×
=
ab,
三角形AEF的面积为:
ab-
ab=
ab,
所以
ab÷ab=
.
答:△AEF的面积是长方形ABCD面积的
.
故答案为:
.
则长方形的面积为:ab,
△ABE、△ADF、四边形AECF的面积都等于
| 1 |
| 3 |
则BE为:
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
同理,DF为:
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
因此三角形FCE的面积为
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 18 |
三角形AEF的面积为:
| 1 |
| 3 |
| 1 |
| 18 |
| 5 |
| 18 |
所以
| 5 |
| 18 |
| 5 |
| 18 |
答:△AEF的面积是长方形ABCD面积的
| 5 |
| 18 |
故答案为:
| 5 |
| 18 |
点评:此题主要考查三角形和长方形的面积的计算方法的灵活应用,利用等量代换的方法即可求解.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图求阴影部分面积
如图求阴影部分面积 (2012?宝应县模拟)如图在长方形ABCD,AB=24厘米,AD=16厘米.一个动点P从顶点A出发,逆时针沿长方形的边以每秒2厘米的速度运动回到A点,(1)P点从A 点出发经过几秒时△ABP面积最大?(2)△ABP面积最大共持续几秒?
(2012?宝应县模拟)如图在长方形ABCD,AB=24厘米,AD=16厘米.一个动点P从顶点A出发,逆时针沿长方形的边以每秒2厘米的速度运动回到A点,(1)P点从A 点出发经过几秒时△ABP面积最大?(2)△ABP面积最大共持续几秒?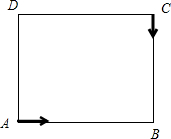
 如图在长方形ABCD,AB=24厘米,AD=16厘米.一个动点P从顶点A出发,逆时针沿长方形的边以每秒2厘米的速度运动回到A点,(1)P点从A 点出发经过几秒时△ABP面积最大?(2)△ABP面积最大共持续几秒?
如图在长方形ABCD,AB=24厘米,AD=16厘米.一个动点P从顶点A出发,逆时针沿长方形的边以每秒2厘米的速度运动回到A点,(1)P点从A 点出发经过几秒时△ABP面积最大?(2)△ABP面积最大共持续几秒?