题目内容
 如图求阴影部分面积
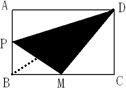
如图求阴影部分面积如图在长方形ABCD中,已知AD=10厘米,AB=8厘米,M是BC边上的中点,P是AB边上的一点,四边形PBMD的面积是30平方厘米,求阴影部分面积.
分析:如图所示,连接DB,由“M是BC边上的中点”可知,S△DBM=
S长方形ABCD,
因长方形的长和宽已知,以及“四边形PBMD的面积是30平方厘米”,进而能求出三角形DPB的面积,于是三角形DPB的面积和高AD已知,就可以求出PB的长度,从而可以求三角形PBM的面积,所以阴影部分的面积=四边形PBMD的面积-三角形PBM的面积,问题得解.
 .
.
| 1 |
| 4 |
因长方形的长和宽已知,以及“四边形PBMD的面积是30平方厘米”,进而能求出三角形DPB的面积,于是三角形DPB的面积和高AD已知,就可以求出PB的长度,从而可以求三角形PBM的面积,所以阴影部分的面积=四边形PBMD的面积-三角形PBM的面积,问题得解.
 .
.解答:解:S△DBM=
×10×8=20(平方厘米),
S△DPB=30-20=10(平方厘米),
又因S△DPB=
×PB×AD,
所以PB=10×2÷10=2(厘米),
则S△PBM=5×2÷2=5(平方厘米),
阴影部分的面积=30-5=25(平方厘米);
答:阴影部分的面积是25平方厘米.
| 1 |
| 4 |
S△DPB=30-20=10(平方厘米),
又因S△DPB=
| 1 |
| 2 |
所以PB=10×2÷10=2(厘米),
则S△PBM=5×2÷2=5(平方厘米),
阴影部分的面积=30-5=25(平方厘米);
答:阴影部分的面积是25平方厘米.
点评:解答此题的关键是连接DB,进而能求出三角形PBM的面积,从而问题得解.

练习册系列答案
相关题目
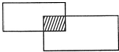 如图,阴影部分是大小两个长方形的重叠部分,小长方形空白部分与阴影部分的面积比是3:1,大长方形空白部分与阴影部分的面积的比5:1.已知小长方形空白部分的面积是36 cm2,求大长方形的面积.
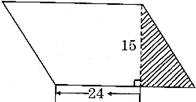
如图,阴影部分是大小两个长方形的重叠部分,小长方形空白部分与阴影部分的面积比是3:1,大长方形空白部分与阴影部分的面积的比5:1.已知小长方形空白部分的面积是36 cm2,求大长方形的面积. (2012?浙江)如图中阴影部分面积为100平方厘米,求两圆之间的环形面积.
(2012?浙江)如图中阴影部分面积为100平方厘米,求两圆之间的环形面积.