题目内容
 如图在长方形ABCD,AB=24厘米,AD=16厘米.一个动点P从顶点A出发,逆时针沿长方形的边以每秒2厘米的速度运动回到A点,(1)P点从A 点出发经过几秒时△ABP面积最大?(2)△ABP面积最大共持续几秒?
如图在长方形ABCD,AB=24厘米,AD=16厘米.一个动点P从顶点A出发,逆时针沿长方形的边以每秒2厘米的速度运动回到A点,(1)P点从A 点出发经过几秒时△ABP面积最大?(2)△ABP面积最大共持续几秒?
解:(1)16÷2=8(秒);
答:P点从A 点出发经过8秒时△ABP面积最大.
(2)24÷2=12(秒),
答:△ABP面积最大共持续12秒.
分析:如图所示,
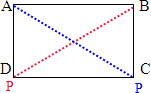
(1)由题意可知:当三角形ABP与长方形ABCD等底等高时,则S△ABP= S长方形ABCD,此时三角形ABP的面积应最大,所以到达D点时面积最大,再用AD的长度除以点P的速度,就可以求出到达D点的时间.
S长方形ABCD,此时三角形ABP的面积应最大,所以到达D点时面积最大,再用AD的长度除以点P的速度,就可以求出到达D点的时间.
(2)当点P离开点C时,面积就减小,所以保持面积最大的距离就是DC的长度,用DC的长度除以速度,就是保持面积最大需要的时间.
点评:解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半.且要明白:当三角形ABP与长方形ABCD等底等高时,三角形ABP的面积最大.
答:P点从A 点出发经过8秒时△ABP面积最大.
(2)24÷2=12(秒),
答:△ABP面积最大共持续12秒.
分析:如图所示,

(1)由题意可知:当三角形ABP与长方形ABCD等底等高时,则S△ABP=
 S长方形ABCD,此时三角形ABP的面积应最大,所以到达D点时面积最大,再用AD的长度除以点P的速度,就可以求出到达D点的时间.
S长方形ABCD,此时三角形ABP的面积应最大,所以到达D点时面积最大,再用AD的长度除以点P的速度,就可以求出到达D点的时间.(2)当点P离开点C时,面积就减小,所以保持面积最大的距离就是DC的长度,用DC的长度除以速度,就是保持面积最大需要的时间.
点评:解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半.且要明白:当三角形ABP与长方形ABCD等底等高时,三角形ABP的面积最大.

练习册系列答案
相关题目
 如图求阴影部分面积
如图求阴影部分面积 (2012?宝应县模拟)如图在长方形ABCD,AB=24厘米,AD=16厘米.一个动点P从顶点A出发,逆时针沿长方形的边以每秒2厘米的速度运动回到A点,(1)P点从A 点出发经过几秒时△ABP面积最大?(2)△ABP面积最大共持续几秒?
(2012?宝应县模拟)如图在长方形ABCD,AB=24厘米,AD=16厘米.一个动点P从顶点A出发,逆时针沿长方形的边以每秒2厘米的速度运动回到A点,(1)P点从A 点出发经过几秒时△ABP面积最大?(2)△ABP面积最大共持续几秒?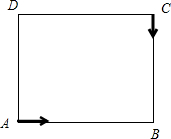
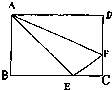 如图在长方形ABCD中,△ABE、△ADF、四边形AECF的面积相等.△AEF的面积是长方形ABCD面积的
如图在长方形ABCD中,△ABE、△ADF、四边形AECF的面积相等.△AEF的面积是长方形ABCD面积的