题目内容
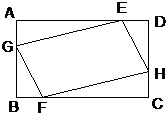 如图.E,F是长方形ABCD长边上的五等分点,G,H是长方形ABCD短边上的三等分点,依次连接E、G、F、H后,得到平行四边形EGFH,已知平行四边形EGFH的面积是21,则长方形ABCD的面积是
如图.E,F是长方形ABCD长边上的五等分点,G,H是长方形ABCD短边上的三等分点,依次连接E、G、F、H后,得到平行四边形EGFH,已知平行四边形EGFH的面积是21,则长方形ABCD的面积是35
35
.分析:由题意可知:长方形的面积-四个小长方形的面积=平行四边形的面积,据此可以列式计算.
解答:解:设ED为a,DH为b,则AE=CF=4a,AG=CH=
,BF=ED=a.
由题意知:ABCD的面积-(三角形AGE的面积+三角形GBF的面积+三角形FCH的面积+三角形HDE的面积)=21;
因为三角形AGE的面积=三角形FCH的面积;三角形GBF的面积=三角形HDE的面积.
所以得到等式:5a×(b+
)-(4a×
÷2×2+a×b÷2×2)=21,
5×
-(2ab+ab)=21,
ab-3ab=21,
ab=21,
ab=
,
长方形的面积=5a×(b+
)=
ab=
×
=35;
故答案为:35.
| b |
| 2 |
由题意知:ABCD的面积-(三角形AGE的面积+三角形GBF的面积+三角形FCH的面积+三角形HDE的面积)=21;
因为三角形AGE的面积=三角形FCH的面积;三角形GBF的面积=三角形HDE的面积.
所以得到等式:5a×(b+
| b |
| 2 |
| b |
| 2 |
5×
| 3b |
| 2 |
| 15 |
| 2 |
| 9 |
| 2 |
ab=
| 14 |
| 3 |
长方形的面积=5a×(b+
| b |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 14 |
| 3 |
故答案为:35.
点评:此题主要考查长方形的面积公式,找清等量关系,就可以列式计算.

练习册系列答案
相关题目
 课外拓展
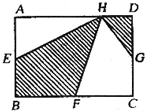
课外拓展 如图,长方形ABCD 中,AB=67,BC=30.E、F分别是AB、BC边上的两点,BE+BF=49.那么,三角形DEF 面积的最小值是
如图,长方形ABCD 中,AB=67,BC=30.E、F分别是AB、BC边上的两点,BE+BF=49.那么,三角形DEF 面积的最小值是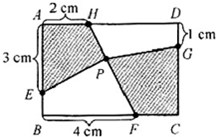 如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取点P,连接EP和GP.当四边形AEPH的面积是5平方厘米时,求四边形PFCG的面积.
如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取点P,连接EP和GP.当四边形AEPH的面积是5平方厘米时,求四边形PFCG的面积. 如图,长方形ABCD的面积是120平方厘米,E是BC边的三等分点,F是DC边的二等分点.求阴影部分的面积.
如图,长方形ABCD的面积是120平方厘米,E是BC边的三等分点,F是DC边的二等分点.求阴影部分的面积.