题目内容
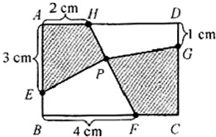 如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取点P,连接EP和GP.当四边形AEPH的面积是5平方厘米时,求四边形PFCG的面积.
如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取点P,连接EP和GP.当四边形AEPH的面积是5平方厘米时,求四边形PFCG的面积.分析:如图所示,连接PB、PD,由题意可知:AH=FC=2cm,HD=BF=4cm,则HF将长方形均分成了2个梯形,所以ABFH的面积和FCDH底面积都为(6×4÷2=12)平方厘米;又因三角形PBF和三角形PHD的底都是4厘米,高的和就等于长方形的宽,于是可以求出二者的面积和,同样的方法可知:三角形PDG和三角形PEB的底都是1厘米,高的和等于长方形的长,也就能求出二者的和,于是就得到了两个空白四边形的面积和,长方形的面积减去已得到的3个四边形的面积就是四边形PFCG的面积.
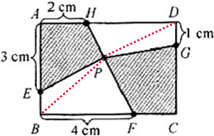

解答:解:长方形ABCD底面积=6×4=24(平方厘米),
梯形ABFH的面积=梯形FCDH的面积=24×
=12(平方厘米),
S△PEB+S△PGD,
=
×1×6,
=3(平方厘米);
S△PBF+S△PDH,
=
×4×4,
=8(平方厘米);
两个空白四边形的面积和为:
8+3=11(平方厘米),
所以四边形PFCG底面积为:
24-11-5=8(平方厘米);
答:四边形PFCG底面积为8平方厘米.
梯形ABFH的面积=梯形FCDH的面积=24×
| 1 |
| 2 |
S△PEB+S△PGD,
=
| 1 |
| 2 |
=3(平方厘米);
S△PBF+S△PDH,
=
| 1 |
| 2 |
=8(平方厘米);
两个空白四边形的面积和为:
8+3=11(平方厘米),
所以四边形PFCG底面积为:
24-11-5=8(平方厘米);
答:四边形PFCG底面积为8平方厘米.
点评:解答此题的关键是:作出辅助线,得出:HF将长方形均分成了2个梯形,求出两个空白四边形的面积和,问题即可得解.

练习册系列答案
相关题目
 如图,有一个长6厘米,宽4厘米的长方形ABCD,已知线段DG、AH、AE、BF的长度依次是1,2,3,4厘米,且四边形AEPH的面积是5平方厘米,且四边形PFCG的面积是多少平方厘米?
如图,有一个长6厘米,宽4厘米的长方形ABCD,已知线段DG、AH、AE、BF的长度依次是1,2,3,4厘米,且四边形AEPH的面积是5平方厘米,且四边形PFCG的面积是多少平方厘米? (2009?西藏)如图,有一个长20厘米,宽15厘米的长方形硬纸,从四个角各剪去一个边长4厘米的正方形后,做成一个无盖的长方体.
(2009?西藏)如图,有一个长20厘米,宽15厘米的长方形硬纸,从四个角各剪去一个边长4厘米的正方形后,做成一个无盖的长方体.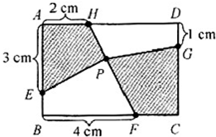 如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取点P,连接EP和GP.当四边形AEPH的面积是5平方厘米时,求四边形PFCG的面积.
如图,有一个宽4厘米、长6厘米的长方形ABCD,在各个边上取点E、F、G、H,在连接H、F的线上取点P,连接EP和GP.当四边形AEPH的面积是5平方厘米时,求四边形PFCG的面积.