题目内容
 如图,长方形ABCD 中,AB=67,BC=30.E、F分别是AB、BC边上的两点,BE+BF=49.那么,三角形DEF 面积的最小值是
如图,长方形ABCD 中,AB=67,BC=30.E、F分别是AB、BC边上的两点,BE+BF=49.那么,三角形DEF 面积的最小值是717
717
.分析:设AE=x,则BE=67-x,BF=49-(67-x)=x-18,CF=30-(x-18)=48-x.
三个直角三角形面积和是
[30x+(67-x)(x-18)+(48-x)67]=
[2010+x(48-x)],要想让三角形DEF面积最小,只需三个直角三角形面积之和最大,显然x=24,则三个直角三角形面积和是
(2010+242)=1293,进行解答即可.
三个直角三角形面积和是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设AE=x,则BE=67-x,BF=49-(67-x)=x-18,CF=30-(x-18)=48-x.
三个直角三角形面积和是
[30x+(67-x)(x-18)+(48-x)67]=
[2010+x(48-x)],
当x=24,则三个直角三角形面积和是
(2010+242)=1293,
则三角形DEF面积是2010-1293=717;
故答案为:717.
三个直角三角形面积和是
| 1 |
| 2 |
| 1 |
| 2 |
当x=24,则三个直角三角形面积和是
| 1 |
| 2 |
则三角形DEF面积是2010-1293=717;
故答案为:717.
点评:此题较难,解答此题的关键是:要想让三角形DEF面积最小,只需三个直角三角形面积之和最大,进而解答即可.

练习册系列答案
相关题目
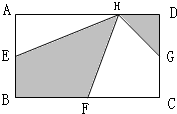 如图,长方形ABCD的面积为60平方厘米,E、F、G分别是AB,BC,CD的中点,H为AD上任意一点,求阴影部分的面积.
如图,长方形ABCD的面积为60平方厘米,E、F、G分别是AB,BC,CD的中点,H为AD上任意一点,求阴影部分的面积. 如图,长方形ABCD中,EF∥AD,GH∥AB,EF和GH相较于点O,长方形OFCH的面积比长方形AEOG的面积大6平方厘米,求三角形OBD的面积.
如图,长方形ABCD中,EF∥AD,GH∥AB,EF和GH相较于点O,长方形OFCH的面积比长方形AEOG的面积大6平方厘米,求三角形OBD的面积. 如图,长方形ABCD,ABEF,AGHF的长与宽的比相同,且
如图,长方形ABCD,ABEF,AGHF的长与宽的比相同,且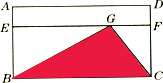
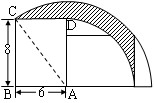 如图,长方形ABCD把这个长方形绕顶点A向右旋转90°,求CD边扫过的阴影部分面积.(单位:厘米)
如图,长方形ABCD把这个长方形绕顶点A向右旋转90°,求CD边扫过的阴影部分面积.(单位:厘米)