题目内容
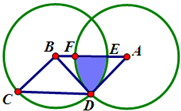 (2012?武汉模拟)如图,两个半径相等的圆A和圆B相交,三角形BCD是等腰直角三角形,其面积为60cm2,四边形ABCD是平行四边形,求图中阴影部分的面积.(π取3.14)
(2012?武汉模拟)如图,两个半径相等的圆A和圆B相交,三角形BCD是等腰直角三角形,其面积为60cm2,四边形ABCD是平行四边形,求图中阴影部分的面积.(π取3.14)分析:ABCD是平行四边形,三角形BCD是等腰直角三角形,所以三角形ABD也是等腰直角三角形,它的面积也是60平方厘米,由此可以求出每个圆半径的平方是多少;阴影部分的面积是两圆重合部分面积的一半,而重合部分由两个相等的弓形组成,我们只需要求出一个弓形面积,就是要求的阴影面积了.连接圆心B和另一个两圆的交点M,以及连接D和M,组成一个扇形;三角形DBM也是等腰直角三角形,那么∠DBA就是45°,一个弓形的圆心角就是90°,再求出圆心角是90°的扇形的面积减去三角形DBM的面积就是一个弓形的面积,也就是阴影部分的面积.
解答:解:连接圆心B和另一个两圆的交点M,以及连接D和M,如图:

阴影部分的面积是一个弓形的面积;
三角形BCD是等腰直角三角形,所以三角形ABD也是等腰直角三角形,它的面积也是60平方厘米,
圆的半径BD的平方就是60×2=120(平方厘米);
∠DBA=45°,
那么∠MBD=90°;
三角形MBD也是一个等腰直角三角形;
弓形DM的面积=扇形DBM的面积-三角形DBM的面积,
×(π×BD2)-
×BD2,
=
×(3.14×120)-
×120,
=94.2-60,
=34.2(平方厘米);
答:阴影部分的面积是34.2平方厘米.

阴影部分的面积是一个弓形的面积;
三角形BCD是等腰直角三角形,所以三角形ABD也是等腰直角三角形,它的面积也是60平方厘米,
圆的半径BD的平方就是60×2=120(平方厘米);
∠DBA=45°,
那么∠MBD=90°;
三角形MBD也是一个等腰直角三角形;
弓形DM的面积=扇形DBM的面积-三角形DBM的面积,
| 90° |
| 360° |
| 1 |
| 2 |
=
| 1 |
| 4 |
| 1 |
| 2 |
=94.2-60,
=34.2(平方厘米);
答:阴影部分的面积是34.2平方厘米.
点评:连接圆心线,与图中的半径组成了等腰直角三角形,从而得出弓形所对的圆心角的度数是解决此类问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目