题目内容
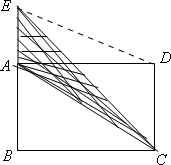
如图所示，长方形ABCD的面积是180平方厘米，CD长15厘米，ED长17厘米，求三角形ACE的面积．
解：连接ED，
AD=BC=180÷15=12（厘米），
AE2=172-122=145（平方厘米），
AE=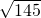
，
三角形ACE的面积是：
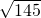×12÷2，
=6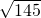（平方厘米）；
答：三角形ACE的面积是6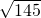平方厘米．
分析：如图所示：
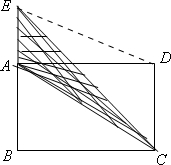
连接ED，因为CD×AD=180，所以AD=180÷15=12（厘米），因为三角形AED是直角三角形，由勾股定理得：在直角三角形里，两条直角边的平方和等于斜边的平方，即AE2+AD2=ED2，所以ED2-AD2=AE2，求出AE的长度，BC或AD的长度就是三角形ACE的高，则三角形ACE的面积=AE×BC÷2，代数计算即可．
点评：解决本题的关键是求出AE的长度，再根据公式计算．
AD=BC=180÷15=12（厘米），
AE2=172-122=145（平方厘米），
AE=
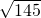，三角形ACE的面积是：
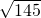×12÷2，=6
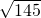（平方厘米）；答：三角形ACE的面积是6
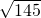平方厘米．分析：如图所示：
连接ED，因为CD×AD=180，所以AD=180÷15=12（厘米），因为三角形AED是直角三角形，由勾股定理得：在直角三角形里，两条直角边的平方和等于斜边的平方，即AE2+AD2=ED2，所以ED2-AD2=AE2，求出AE的长度，BC或AD的长度就是三角形ACE的高，则三角形ACE的面积=AE×BC÷2，代数计算即可．
点评：解决本题的关键是求出AE的长度，再根据公式计算．
练习册系列答案
相关题目
课外拓展
如图所示，长方形ABCD中，AB=14厘米，AD=12厘米，现沿其对角线BD将它对折，得一几何图形，则图中阴影部分周长是
如图所示，某桌球桌面为长方形ABCD，小球从A沿45°角击出，恰好经过5次碰撞到达B处．则 AB：BC=
如图所示，长方形ABCD中，三角形ABD的面积比三角形BCD的面积大10平方厘米，且AB=8厘米，CD=3厘米，求图中阴影部分的面积．
如图所示，长方形ABCD中，AD长6cm，AB长5cm，△ADE、四边形DEBF及△CDF的面积分别相等，则△DEF的面积为