题目内容
5.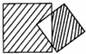 如图,小正方形的$\frac{3}{4}$被阴影部分覆盖,大正方形的$\frac{6}{7}$被阴影部分覆盖,小正方形的阴影部分面积与大正方形的阴影部分面积之比是1:2.
如图,小正方形的$\frac{3}{4}$被阴影部分覆盖,大正方形的$\frac{6}{7}$被阴影部分覆盖,小正方形的阴影部分面积与大正方形的阴影部分面积之比是1:2.
分析 由题意可知:重叠部分占小正方形的四分之一,重叠部分占大正方形的七分之一,所以小正方形的面积的四分之一等于大正方形面积的七分之一,即小正方形面积×$\frac{1}{4}$=大正方形面积×$\frac{1}{7}$,根据比例的基本性质,可求出小正方形面积与大正方形面积面积的比,进而求出小正方形的阴影部分与大正方形阴影部分面积之比.
解答 解:小正方形面积×(1-$\frac{3}{4}$)=大正方形面积×(1-$\frac{6}{7}$),
即小正方形面积×$\frac{1}{4}$=大正方形面积×$\frac{1}{7}$,
所以小正方形面积:大正方形面积=$\frac{1}{7}$:$\frac{1}{4}$=4:7,
则小正方形面积是4份,大正方形面积是7份,
小正方形与大正方形面积之比为4:7;
所以小正方形被阴影部分覆盖就是4×$\frac{3}{4}$=3份,大正方形被阴影部分覆盖就是7×$\frac{6}{7}$=6份,
小正方形的阴影部分与大正方形阴影部分面积之比是3:6=1:2,
故答案为:1:2.
点评 解答此题的关键是求出大小正方形的面积之比,然后求出大小正方形被阴影部分覆盖的分数,然后相比即可.

练习册系列答案
相关题目
10.甲、乙两个同学沿着不同的圆形跑道跑步.甲每分跑120米,乙每分跑240米.两人同时起跑,经过相同的时间,都跑了各自的一圈.下面说法正确的是( )
| A. | 甲跑的图形跑道周长是乙的一半 | B. | 两个圆形跑道的周长比是1:1 | ||
| C. | 两个圆的面积比是2:1 | D. | 甲跑的圆的面积是乙的一半 |
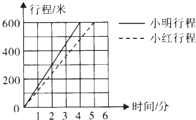 如图是小明和小红两人600米赛跑的行程图.
如图是小明和小红两人600米赛跑的行程图.