题目内容
一个分数，它的分母加上3可约分为
，它的分母减去2可约分为
，这个分数是多少？
| 3 |
| 7 |
| 2 |
| 3 |
分析：可以假设这个分数是
，则有
=
，即a=
；
=
，即a=
；因此
=
，解方程，即可得解．
| a |
| b |
| a |
| b+3 |
| 3 |
| 7 |
| 3b+9 |
| 7 |
| a |
| b-2 |
| 2 |
| 3 |
| 2b-4 |
| 3 |
| 3b+9 |
| 7 |
| 2b-4 |
| 3 |
解答：解：设这个分数是
，则有
=
，即a=
；
=
，即a=
；
因此：
=
，
则：9b+27=14b-28，
5b=55，
b=11；
（3×11+9）÷7=6，
所以原分数为
；
答：这个分数是
．
| a |
| b |
| a |
| b+3 |
| 3 |
| 7 |
| 3b+9 |
| 7 |
| a |
| b-2 |
| 2 |
| 3 |
| 2b-4 |
| 3 |
因此：
| 3b+9 |
| 7 |
| 2b-4 |
| 3 |
则：9b+27=14b-28，
5b=55，
b=11；
（3×11+9）÷7=6，
所以原分数为
| 6 |
| 11 |
答：这个分数是
| 6 |
| 11 |
点评：灵活应用约分和通分的性质，分子、分母同时乘或除以一个非0的数，值不变来解决实际问题．
练习册系列答案
相关题目
，分子减5可化简为
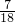，求这个数．
+
×
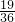
，分子减7，化简后为
；它的分母减2，可以约简为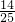
．这个分数是________．