题目内容
【题目】小军是个“科学迷”,在一次课外探究实验中,小军在底面积为![]() 的空圆柱形容器内水平放置由两个实心圆柱组成的“几何体”(如图①)。他向容器内匀速注水,注满为止。在注水过程中,小军发现水面高度
的空圆柱形容器内水平放置由两个实心圆柱组成的“几何体”(如图①)。他向容器内匀速注水,注满为止。在注水过程中,小军发现水面高度![]() 与注水时间
与注水时间![]() 之间的关系如图②所示。请根据图中提供的信息,解答下列问题:
之间的关系如图②所示。请根据图中提供的信息,解答下列问题:
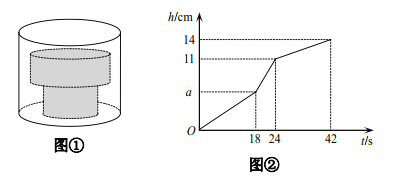
(1)圆柱形容器的高为______![]() ,匀速注水的水流速度为______
,匀速注水的水流速度为______![]() (直接写出答案);
(直接写出答案);
(2)若“几何体”的下方圆柱的底面积为![]() ,请帮助小军求出“几何体”上方圆柱的高和底面积。
,请帮助小军求出“几何体”上方圆柱的高和底面积。
【答案】(1)14;5。(2)5cm,24cm。
【解析】
(1)根据水面高度h(cm)与注水时间t(s)之间的关系,可得圆柱形容器的高为14cm;然后用圆柱形容器的底面积乘以两个实心圆柱组成的“几何体”的顶部到容器的顶部的距离,再除以水从刚满过由两个实心圆柱组成的“几何体”到注满用的时间,求出匀速注水的水流速度为多少即可。
(2)首先根据圆柱的体积公式,求出“几何体”下方圆柱的高为多少,再用“几何体”的高减去“几何体”下方圆柱的高,求出“几何体”上方圆柱的高是多少;然后设“几何体”上方圆柱的底面积为Scm,则5×(30-S)=5×(24-18),据此求出S的值是多少即可。
圆柱体积=底面积×高,注水的水流速度=注水体积÷注水时间。
(1)水面高度h(cm)与注水时间t(s)之间的关系,可得圆柱形的容器的高为14cm。
水流速度:30×(14-11)÷(42-24)
=30×3÷18
=5(cm/s)
即圆柱形容器的高为14cm,匀速注水的水流速度为5 cm/s。
(2)“几何体”上方圆柱的高为:
11-(5×18)÷(30-15)
=11-90÷15
=11-6
=5(cm)
解:设“几何体”上方圆柱的底面积为Scm。
则5×(30-S)=5×(24-18)
150-5S=30
150-5S+5S=30+5S
30+5S=150
5S=150-30
5S=120
S=120÷5
S=24
答:“几何体”上方圆柱的高为5cm,底面积24cm。

 阅读快车系列答案
阅读快车系列答案