题目内容
8.在一根长100厘米的木棍上,从左到右每隔6厘米涂一个红点,再从左至右每隔5厘米也涂一个红点,然后在每个红点处把木棍一一锯开.那么锯出的长1厘米的小木棍有7根.分析 因为100能被5整除,所以自右至左染色也就是自左至右染色.于是我们可以看作是从同一端点染色.
6与5的最小公倍数是30,即在30厘米的地方,同时染上红色,这样染色就会出现循环,每一周的长度是30厘米,如图所示.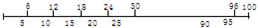
由图示可知长1厘米的短木棍,每一周期中有两段,如第1周期中,6-5=1,5×5-6×4=1.剩余10厘米中有一段.所以锯开后长1厘米的短木棍共有7段.
解答 解:2×[(100-10)÷30]+1
=2×3+1
=7(段)
答:那么长度是1厘米的短木棍有7根.
故答案为:7.
点评 解决这一问题的关键是根据整除性把自右向左每隔5厘米的染色,转化为自左向右的染色,便于利用最小公倍数发现周期现象,化难为易.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
13.某商场购进一批洗衣机,然后按零售价卖出,当卖出这批洗衣机的90%时,商场已或利润15000元.
(1)商场购进的这批洗衣机一共有多少台?
(2)当这批洗衣机全部卖出时,商场可获利润多少元?
| 购进价/元 | 零售价/元 |
| 2200 | 2500 |
(2)当这批洗衣机全部卖出时,商场可获利润多少元?
