题目内容
一个圆柱体削去一个最大的长方体,体积减少了114立方厘米,求圆柱体的体积?
解:根据题干分析可得:设圆柱和长方体的高是h,圆柱的底面直径是2r,半径就是r,
则圆柱的体积是:πr2h;
圆柱内最大的长方体的体积是:2r×r÷2×2×h=2r2h;
所以这个长方体的体积是圆柱的体积的:2r2h÷πr2h= ;
;
所以圆柱的体积是114÷ =114×
=114×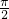 =178.98(立方厘米),
=178.98(立方厘米),
答:圆柱的体积是178.98立方厘米.
分析:根据圆柱内最大的长方体的特征可得:这个长方体的高与圆柱的高相等,长方体的底面积是圆柱的底面圆中最大的正方形,且这个正方形的对角线的长度等于圆柱的底面直径,由此求出这个最大的长方体的体积是圆柱的体积的几分之几,再利用分数除法的意义即可解答问题.
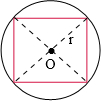
点评:根据圆柱内最大的长方体的特点,求出长方体与圆柱的体积之间的关系,是解决本题的关键.
则圆柱的体积是:πr2h;
圆柱内最大的长方体的体积是:2r×r÷2×2×h=2r2h;
所以这个长方体的体积是圆柱的体积的:2r2h÷πr2h=
 ;
;所以圆柱的体积是114÷
 =114×
=114×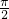 =178.98(立方厘米),
=178.98(立方厘米),答:圆柱的体积是178.98立方厘米.
分析:根据圆柱内最大的长方体的特征可得:这个长方体的高与圆柱的高相等,长方体的底面积是圆柱的底面圆中最大的正方形,且这个正方形的对角线的长度等于圆柱的底面直径,由此求出这个最大的长方体的体积是圆柱的体积的几分之几,再利用分数除法的意义即可解答问题.

点评:根据圆柱内最大的长方体的特点,求出长方体与圆柱的体积之间的关系,是解决本题的关键.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目