题目内容
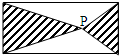 点P是长方形内任意一点,阴影部分的总面积与空白部分总面积比较
点P是长方形内任意一点,阴影部分的总面积与空白部分总面积比较
- A.S阴>S白
- B.S阴<S白
- C.S阴=S白
C
分析:为了便于表示添加了两条线段和四个点(如下图),要比较阴影部分的总面积与空白部分总面积,需要利用三角形的面积公式空白部分总面积=三角形APD的面积+三角形BCP的面积,阴影部分的总面积=三角形APB的面积+三角形DCP的面积,然后进行比较.
解答:根据题意和三角形的面积公式得:
空白部分的总面积=三角形APD的面积+三角形BCP的面积
=AD×PE÷2+BC×PF÷2
=AD×(PE+PF)÷2
=AD×EF÷2;
阴影部分的总面积=三角形APB的面积+三角形DCP的面积
=AB×PG÷2+CD×PH÷2
=AB×(PG+PH)÷2
=AB×GH÷2;
由题意和图可知:AB=EF,AD=GH,
所以阴影部分的总面积=空白部分的总面积;
故选:C.

点评:解此题的关键是把阴影部分的总面积和空白部分的总面积转化成与长方形的长和宽相关的式子.
分析:为了便于表示添加了两条线段和四个点(如下图),要比较阴影部分的总面积与空白部分总面积,需要利用三角形的面积公式空白部分总面积=三角形APD的面积+三角形BCP的面积,阴影部分的总面积=三角形APB的面积+三角形DCP的面积,然后进行比较.
解答:根据题意和三角形的面积公式得:
空白部分的总面积=三角形APD的面积+三角形BCP的面积
=AD×PE÷2+BC×PF÷2
=AD×(PE+PF)÷2
=AD×EF÷2;
阴影部分的总面积=三角形APB的面积+三角形DCP的面积
=AB×PG÷2+CD×PH÷2
=AB×(PG+PH)÷2
=AB×GH÷2;
由题意和图可知:AB=EF,AD=GH,
所以阴影部分的总面积=空白部分的总面积;
故选:C.

点评:解此题的关键是把阴影部分的总面积和空白部分的总面积转化成与长方形的长和宽相关的式子.

练习册系列答案
相关题目
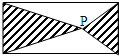 (2008?扬州)点P是长方形内任意一点,阴影部分的总面积与空白部分总面积比较( )
(2008?扬州)点P是长方形内任意一点,阴影部分的总面积与空白部分总面积比较( )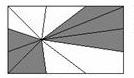 将长15厘米,宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连接,如图,则阴影部分的面积是
将长15厘米,宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连接,如图,则阴影部分的面积是 将长12厘米,宽9厘米的长方形的长二等分,宽三等分,长方形内任意一点与分点或顶点连接,如图所示.求阴影部分的面积.
将长12厘米,宽9厘米的长方形的长二等分,宽三等分,长方形内任意一点与分点或顶点连接,如图所示.求阴影部分的面积.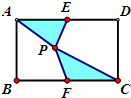 如图,ABCD是长为8,宽为6的长方形E、F分别是AD、BC的中点,P为长方形内任一点,求阴影部分的面积?
如图,ABCD是长为8,宽为6的长方形E、F分别是AD、BC的中点,P为长方形内任一点,求阴影部分的面积?