题目内容
 将长12厘米,宽9厘米的长方形的长二等分,宽三等分,长方形内任意一点与分点或顶点连接,如图所示.求阴影部分的面积.
将长12厘米,宽9厘米的长方形的长二等分,宽三等分,长方形内任意一点与分点或顶点连接,如图所示.求阴影部分的面积.分析:分别求各阴影部分面积,再将两部分面积相加.
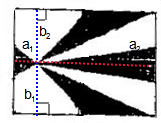
如图所示,过所有三角形的公共顶点分别向长方形的四条边作垂线,它们的长分别a1厘米、b1厘米、a2厘米、b2厘米,则横向的阴影部分的面积是
×(9×
)×(a1+a2)平方厘米;同理纵向的阴影部分的面积是
×(
×12)×(b1+b2),从而问题得解.

如图所示,过所有三角形的公共顶点分别向长方形的四条边作垂线,它们的长分别a1厘米、b1厘米、a2厘米、b2厘米,则横向的阴影部分的面积是
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:据分析解答如下:
×(
×9)×12+
×(
×12)×9,
=
×3×12+
×6×9,
=3×6+3×9,
=18+27,
=45(平方厘米);
答:阴影部分的面积是45平方厘米.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=3×6+3×9,
=18+27,
=45(平方厘米);
答:阴影部分的面积是45平方厘米.
点评:此题解答的关键是先作出辅助线,然后分别求各阴影部分面积,再将两部分面积相加即可得出结论.

练习册系列答案
相关题目