题目内容
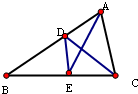 图三角形ABC中,三角形BDE,DCE,ACD的面积分别是90,30,28平方厘米.求三角形ADE的面积?
图三角形ABC中,三角形BDE,DCE,ACD的面积分别是90,30,28平方厘米.求三角形ADE的面积?
解:因为S△BDE=90平方厘米,S△DCE=30平方厘米,
则BE:EC=90:30=3:1,
又因S△ABC=90+30+28=148平方厘米,
三角形ABE的面积为:148× =111(平方厘米),
=111(平方厘米),
三角形ADE的面积=111-90=21(平方厘米).
答:三角形ADE的面积是21平方厘米.
分析:由题意可知:S△ABC=90+30+28=148平方厘米,而三角形BDE和三角形DCE、三角形ABE和三角形AEC是等高不等底的三角形,则其对应底的比应等于其面积比,S△BDE=90平方厘米,S△DCE=30平方厘米,则可以求出BE与EC的比,进而可以求出三角形ABE的面积,S△ADE=S△ABE-S△BDE.
点评:解答此题的主要依据是:等高不等底的三角形的对应底的比等于其面积比.
则BE:EC=90:30=3:1,
又因S△ABC=90+30+28=148平方厘米,
三角形ABE的面积为:148×
 =111(平方厘米),
=111(平方厘米),三角形ADE的面积=111-90=21(平方厘米).
答:三角形ADE的面积是21平方厘米.
分析:由题意可知:S△ABC=90+30+28=148平方厘米,而三角形BDE和三角形DCE、三角形ABE和三角形AEC是等高不等底的三角形,则其对应底的比应等于其面积比,S△BDE=90平方厘米,S△DCE=30平方厘米,则可以求出BE与EC的比,进而可以求出三角形ABE的面积,S△ADE=S△ABE-S△BDE.
点评:解答此题的主要依据是:等高不等底的三角形的对应底的比等于其面积比.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 在三角形ABC中,D是BC的一个三等分点,E是AC的中点,AD和BE把三角形分成四块,其面积分别为S1、S2、S3、S4(如图所思)已知S1比S2大7平方厘米,S3的面积为18平方厘米;求△ABC的面积.
在三角形ABC中,D是BC的一个三等分点,E是AC的中点,AD和BE把三角形分成四块,其面积分别为S1、S2、S3、S4(如图所思)已知S1比S2大7平方厘米,S3的面积为18平方厘米;求△ABC的面积.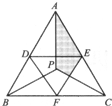 在面积为120平方厘米的等边三角形ABC中,由P点与三个顶点A、B、C连接并形成三个完全相同的三角形.D、E、F分别是△ABC三边上的中点,相连后又形成一个三角形.问图中阴影部分的面积是多少平方厘米?
在面积为120平方厘米的等边三角形ABC中,由P点与三个顶点A、B、C连接并形成三个完全相同的三角形.D、E、F分别是△ABC三边上的中点,相连后又形成一个三角形.问图中阴影部分的面积是多少平方厘米? (2012?长清区模拟)如图:在三角形ABC中,D是BC的中点,E、F是AC的三等分点,已知三角形ABC的面积是108平方厘米,三角形CDF的面积是多少平方厘米?
(2012?长清区模拟)如图:在三角形ABC中,D是BC的中点,E、F是AC的三等分点,已知三角形ABC的面积是108平方厘米,三角形CDF的面积是多少平方厘米?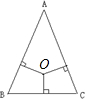 如图,三角形ABC中有一点O,O点到三条边的垂线段长都是3厘米.又知道三角形的周长是30厘米,那么三角形ABC的面积是
如图,三角形ABC中有一点O,O点到三条边的垂线段长都是3厘米.又知道三角形的周长是30厘米,那么三角形ABC的面积是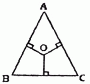 如图,在三角形ABC中有一点O,O点到三条边的垂线长都是2厘米,又知道三角形的周长是20厘米,那么三角形ABC的面积是
如图,在三角形ABC中有一点O,O点到三条边的垂线长都是2厘米,又知道三角形的周长是20厘米,那么三角形ABC的面积是