题目内容
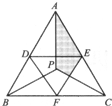 在面积为120平方厘米的等边三角形ABC中,由P点与三个顶点A、B、C连接并形成三个完全相同的三角形.D、E、F分别是△ABC三边上的中点,相连后又形成一个三角形.问图中阴影部分的面积是多少平方厘米?
在面积为120平方厘米的等边三角形ABC中,由P点与三个顶点A、B、C连接并形成三个完全相同的三角形.D、E、F分别是△ABC三边上的中点,相连后又形成一个三角形.问图中阴影部分的面积是多少平方厘米?分析:(1)因为“D、E、F分别是△ABC三边上的中点,”所以△DEF与△ABC相似,相似比是1:2,则它们的面积比就是1:4,所以△DEF的面积=120÷4=30平方厘米;又因为“P点与三个顶点A、B、C连接并形成三个完全相同的三角形”所以P是等边三角形ABC的中心,则△APC的面积=120÷3=40平方厘米;
(2)观察图形不难得出,点P也是△DEF的中心,所以图中3、4、5部分的面积相等是:30÷3=10平方厘米;则1和2部分的面积相等是(40-10)÷2=15平方厘米;由此即可求出1与3部分的面积之和是10+15=25平方厘米,即阴影部分的面积.
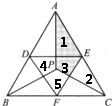
(2)观察图形不难得出,点P也是△DEF的中心,所以图中3、4、5部分的面积相等是:30÷3=10平方厘米;则1和2部分的面积相等是(40-10)÷2=15平方厘米;由此即可求出1与3部分的面积之和是10+15=25平方厘米,即阴影部分的面积.

解答:解:因为“D、E、F分别是△ABC三边上的中点,”
所以△DEF与△ABC相似,相似比是1:2,则它们的面积比就是1:4,
所以△DEF的面积=120÷4=30(平方厘米);
又因为“P点与三个顶点A、B、C连接并形成三个完全相同的三角形”
所以P是等边三角形ABC的中心,则△APC的面积=120÷3=40(平方厘米);
点P也是△DEF的中心,所以图中3、4、5部分的面积相等是:30÷3=10(平方厘米);
则1和2部分的面积相等是(40-10)÷2=15(平方厘米);
则阴影部分的面积是:10+15=25(平方厘米),
答:阴影部分的面积是25平方厘米.
所以△DEF与△ABC相似,相似比是1:2,则它们的面积比就是1:4,
所以△DEF的面积=120÷4=30(平方厘米);
又因为“P点与三个顶点A、B、C连接并形成三个完全相同的三角形”
所以P是等边三角形ABC的中心,则△APC的面积=120÷3=40(平方厘米);
点P也是△DEF的中心,所以图中3、4、5部分的面积相等是:30÷3=10(平方厘米);
则1和2部分的面积相等是(40-10)÷2=15(平方厘米);
则阴影部分的面积是:10+15=25(平方厘米),
答:阴影部分的面积是25平方厘米.
点评:此题考查了三角形的三条中位线围成的三角形与原三角形相似以及等边三角形的中心的性质,关键是找出图形中面积相等的几个部分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
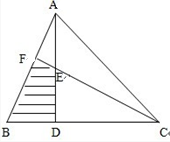 如图,在三角形ABC中,BD:DC=1:2,E为AD的中点,若三角形ABC的面积为120平方厘米,则阴影部分的面积是多少平方厘米?
如图,在三角形ABC中,BD:DC=1:2,E为AD的中点,若三角形ABC的面积为120平方厘米,则阴影部分的面积是多少平方厘米?