题目内容
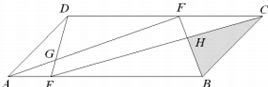 图中,ABCD是平行四边形,E在AB边上,F在DC边上,G为AF与DE的交点,H为CE与BF的交点.已知,平行四边形ABCD的面积是1,
图中,ABCD是平行四边形,E在AB边上,F在DC边上,G为AF与DE的交点,H为CE与BF的交点.已知,平行四边形ABCD的面积是1,| AE |
| EB |
| 1 |
| 4 |
| 1 |
| 8 |
分析:设出平行四边形的底和高,得出F点的位置,进而用平行四边形的底表示出CF、DF、BE、AE的长度,进而用平行四边形的底和高与三角形ADG的底和高的关系,问题即可得解.
解答:解:设平行四边形ABCD的底为a,高为h,ah=1.
AE=
,BE=
,h=
.
1.计算F点在CD上的位置:
S△BEH=BE×h÷2-S△BCH,
=
a×
-
,
=
;
h1=2×S△BEH÷BE(h1为△BEH之BE边上的高),
=2×
÷
a,
=
;
S△CFH=CF×(h-h1)÷2,
=CF×h÷2-S△BCH,
所以CF×(
-
)÷2=CF×
÷2-
,
CF×
=CF×
-
,
CF×
=
,
CF=
;
DF=DC-CF=
;
2.计算△ADG的面积:
S△ADG=S△ADE-S△AEG,
=AE×h÷2-AE×h2÷2,(h2为△AEG之AE边上的高)
=
×
÷2-
×h2÷2,
=
-
×h2,(1)
S△ADG=S△ADF-S△DFG,
=DF×h÷2-DF×(h-h2)÷2,
=(DF×h2)÷2,
=
×h2÷2,
=
×h2,(2)
(2)代入(1)可得:
×h2=
-
×h2,
×h2=
-
×h2,
h2=
,
S△ADG=
×h2,
=
×
,
=
;
答:△ADG的面积是
.
AE=
| a |
| 5 |
| 4a |
| 5 |
| 1 |
| a |
1.计算F点在CD上的位置:
S△BEH=BE×h÷2-S△BCH,
=
| 4 |
| 5 |
| 1 |
| 2a |
| 1 |
| 8 |
=
| 11 |
| 40 |
h1=2×S△BEH÷BE(h1为△BEH之BE边上的高),
=2×
| 11 |
| 40 |
| 4 |
| 5 |
=
| 55 |
| 80a |
S△CFH=CF×(h-h1)÷2,
=CF×h÷2-S△BCH,
所以CF×(
| 1 |
| a |
| 55 |
| 80a |
| 1 |
| a |
| 1 |
| 8 |
CF×
| 25 |
| 160a |
| 80 |
| 160a |
| 20 |
| 160 |
CF×
| 55 |
| 160a |
| 20 |
| 160 |
CF=
| 4a |
| 11 |
DF=DC-CF=
| 7a |
| 11 |
2.计算△ADG的面积:
S△ADG=S△ADE-S△AEG,
=AE×h÷2-AE×h2÷2,(h2为△AEG之AE边上的高)
=
| a |
| 5 |
| 1 |
| a |
| a |
| 5 |
=
| 1 |
| 10 |
| a |
| 10 |
S△ADG=S△ADF-S△DFG,
=DF×h÷2-DF×(h-h2)÷2,
=(DF×h2)÷2,
=
| 7a |
| 11 |
=
| 7a |
| 22 |
(2)代入(1)可得:
| 7a |
| 22 |
| 1 |
| 10 |
| a |
| 10 |
| 70a |
| 220 |
| 22 |
| 220 |
| 22a |
| 220 |
h2=
| 22 |
| 92a |
S△ADG=
| 7a |
| 22 |
=
| 7a |
| 22 |
| 22 |
| 92a |
=
| 7 |
| 92 |
答:△ADG的面积是
| 7 |
| 92 |
点评:此题难度较大,关键是得出平行四边形的底和高与三角形ADG的底和高的关系,问题即可得解.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
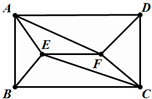 右图中,ABCD是长方形,EF平行于BC,四边形AECF的面积是17.5,三角形AFD的面积是20,三角形BCE的面积是15,三角形CDF的面积是12.5,问三角形ABE的面积是多少?
右图中,ABCD是长方形,EF平行于BC,四边形AECF的面积是17.5,三角形AFD的面积是20,三角形BCE的面积是15,三角形CDF的面积是12.5,问三角形ABE的面积是多少?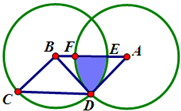 (2012?武汉模拟)如图,两个半径相等的圆A和圆B相交,三角形BCD是等腰直角三角形,其面积为60cm2,四边形ABCD是平行四边形,求图中阴影部分的面积.(π取3.14)
(2012?武汉模拟)如图,两个半径相等的圆A和圆B相交,三角形BCD是等腰直角三角形,其面积为60cm2,四边形ABCD是平行四边形,求图中阴影部分的面积.(π取3.14)
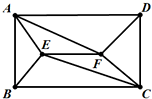 右图中,ABCD是长方形,EF平行于BC,四边形AECF的面积是17.5,三角形AFD的面积是20,三角形BCE的面积是15,三角形CDF的面积是12.5,问三角形ABE的面积是多少?
右图中,ABCD是长方形,EF平行于BC,四边形AECF的面积是17.5,三角形AFD的面积是20,三角形BCE的面积是15,三角形CDF的面积是12.5,问三角形ABE的面积是多少?