题目内容
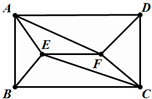右图中，ABCD是长方形，EF平行于BC，四边形AECF的面积是17.5，三角形AFD的面积是20，三角形BCE的面积是15，三角形CDF的面积是12.5，问三角形ABE的面积是多少？分析：因为：△AFD的面积与△BCE的面积和等于长方形面积的一半，由此求出长方形的面积，进而求出三角形ABE的面积
解答：解：△AFD的吗+△BCE的面积=长方形面积的一半=20+15=35，
所以长方形的面积=35×2=70，
所以△ABE的面积=70-17.5-20-15-12.5=5．
答：三角形ABE的面积是5．
所以长方形的面积=35×2=70，
所以△ABE的面积=70-17.5-20-15-12.5=5．
答：三角形ABE的面积是5．
点评：关键是根据图得出：△AFD的面积与△BCE的面积和等于长方形面积的一半．
练习册系列答案
相关题目
图中，四边形ABCD都是边长为1的正方形，E、F、G、H分别是AB、BC、CD、DA的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数
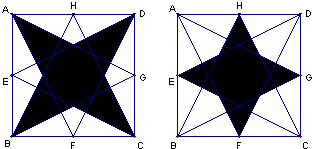右图中，四边形ABCD都是边长为1的正方形，E、F、G、H分别是AB、BC、CD、DA的中点，左图中阴影部分是右图中阴影部分的面积
下图中，四边形ABCD都是边长为1的正方形，E、F、G、H分别是AB、BC、CD、DA的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数
奥运会即将开幕了，全市掀起了美化城市的热潮．有位同学为一家商店设计了一副霓虹灯闪烁的原理图．
奥运会即将开幕了，全市掀起了美化城市的热潮．有位同学为一家商店设计了一副霓虹灯闪烁的原理图．