题目内容
 如图,已知∠AOB=120°.点C在∠AOB的内部,且∠BOC=30°;OP是∠AOB的角平分线.
如图,已知∠AOB=120°.点C在∠AOB的内部,且∠BOC=30°;OP是∠AOB的角平分线.(1)作∠BOC;
(2)尺规作图:作∠AOB的角平分线OP;(不写作法,保留作图痕迹.)
(3)若射线OC、OA分别表示从点O出发的北、东两个方向,则射线OB表示
北偏西30°
北偏西30°
方向;(4)在图中找出与∠AOP互余的角是
∠BOC和∠COP
∠BOC和∠COP
;(5)在图中找出与∠AOB互补的角是
∠AOP和∠BOP
∠AOP和∠BOP
.分析:(1)以OB为边,在∠AOB的内部画∠BOC=30°;
(2)利用尺规作图的方法,作∠AOB的角平分线OP;
(3)把OC、OA看做方向标,那么OB指的是北偏西30°方向;
(4)互余角是指两角角度和为90度,这两个角叫互为余角,据此找出;
(5)互补角是指两角角度和为180度,这两个角叫互为补角,根据图形中角的度数特点即可解决.
(2)利用尺规作图的方法,作∠AOB的角平分线OP;
(3)把OC、OA看做方向标,那么OB指的是北偏西30°方向;
(4)互余角是指两角角度和为90度,这两个角叫互为余角,据此找出;
(5)互补角是指两角角度和为180度,这两个角叫互为补角,根据图形中角的度数特点即可解决.
解答:解:(1)以OB为边,在∠AOB的内部画∠BOC=30°,如图所示;
(2)画出∠AOB的角平分线OP如图所示;
(3)把射线OC、OA看做方向标,分别表示从点O出发的北、东两个方向,则射线OB表示北偏西30°方向;
(4)∠BOC=30°,∠AOP=∠BOP=60°,则∠C0P=60°-30°=30°,
所以可得:∠AOP+∠BOC=90°,∠AOP+∠COP=90°
所以∠AOP的余角是∠BOC和∠COP;
(5)因为∠AOB=120°所以∠AOB+∠AOP=180°,∠AOB+∠BOP=180°,
所以∠AOB的补角是:∠AOP和∠BOP.
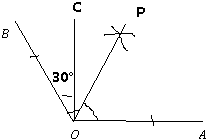
故答案为:(3)北偏西30°;(4)∠BOC和∠COP;(5)∠AOP和∠BOP.
(2)画出∠AOB的角平分线OP如图所示;
(3)把射线OC、OA看做方向标,分别表示从点O出发的北、东两个方向,则射线OB表示北偏西30°方向;
(4)∠BOC=30°,∠AOP=∠BOP=60°,则∠C0P=60°-30°=30°,
所以可得:∠AOP+∠BOC=90°,∠AOP+∠COP=90°
所以∠AOP的余角是∠BOC和∠COP;
(5)因为∠AOB=120°所以∠AOB+∠AOP=180°,∠AOB+∠BOP=180°,
所以∠AOB的补角是:∠AOP和∠BOP.

故答案为:(3)北偏西30°;(4)∠BOC和∠COP;(5)∠AOP和∠BOP.
点评:此题考查了画已知度数的角;利用尺规作图画角的平分线;根据方向标和角的度数表示方向;以及求一个角的余角和补角的方法的灵活应用.

练习册系列答案
相关题目
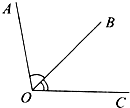 如图,已知∠AOB=55°,∠BOC=45°.求∠AOC的度数.
如图,已知∠AOB=55°,∠BOC=45°.求∠AOC的度数.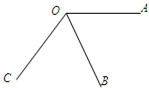 如图,已知∠AOB=58°,∠BOC=(x+5)°,∠AOC=(2x-7)°,那么∠AOC=
如图,已知∠AOB=58°,∠BOC=(x+5)°,∠AOC=(2x-7)°,那么∠AOC=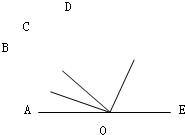 如图,已知∠AOB=∠BOC,∠COD=∠DOE,A、O、E、三个点在同一条直线上.求∠BOD的度数.
如图,已知∠AOB=∠BOC,∠COD=∠DOE,A、O、E、三个点在同一条直线上.求∠BOD的度数.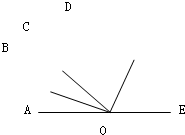 如图,已知∠AOB=∠BOC,∠COD=∠DOE,A、O、E、三个点在同一条直线上.求∠BOD的度数.
如图,已知∠AOB=∠BOC,∠COD=∠DOE,A、O、E、三个点在同一条直线上.求∠BOD的度数.