题目内容
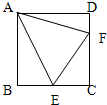 (2013?武侯区模拟)如图,ABCD是正方形,E是BC边的中点,三角形ECF与三角形ADF面积一样大,那么三角形AEF(阴影部分)面积是正方形面积的百分之
(2013?武侯区模拟)如图,ABCD是正方形,E是BC边的中点,三角形ECF与三角形ADF面积一样大,那么三角形AEF(阴影部分)面积是正方形面积的百分之四十一点六七
四十一点六七
.(结果保留两位小数).分析:由图可知:设正方形的边长为a,则三角形ECF的面积为
×
a×FC=
aFC,三角形ADF的面积为
aDF,又因三角形ECF与三角形ADF面积一样大,即
aFC=
aDF,则DF:FC=1:2,所以DF=
a,FC=
a,进而用正方形的面积减去周围3个三角形的面积,就是阴影部分的面积,从而问题得解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
解答:解:设正方形的边长为a,则三角形ECF的面积为
×
a×FC=
aFC,三角形ADF的面积为
aDF,
又因三角形ECF与三角形ADF面积一样大,
即
aFC=
aDF,
则DF:FC=1:2,
所以DF=
a,FC=
a,
阴影部分的面积为:a2-
a×
×a-
a×
×
a-
×a×
×
a,
=a2-
a2-
a2-
a2,
=
a2,
a2÷a2≈41.67%,
答:三角形AEF(阴影部分)面积是正方形面积的41.67%.
故答案为:四十一点六七.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
又因三角形ECF与三角形ADF面积一样大,
即
| 1 |
| 4 |
| 1 |
| 2 |
则DF:FC=1:2,
所以DF=
| 1 |
| 3 |
| 2 |
| 3 |
阴影部分的面积为:a2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
=a2-
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 6 |
=
| 5 |
| 12 |
| 5 |
| 12 |
答:三角形AEF(阴影部分)面积是正方形面积的41.67%.
故答案为:四十一点六七.
点评:求出DF、FC与正方形的边长的关系,是解答本题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 (2013?武侯区模拟)在图的正方体上切一刀,使切面成为一个最大的等边三角形.
(2013?武侯区模拟)在图的正方体上切一刀,使切面成为一个最大的等边三角形.