题目内容
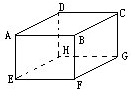 在正方体的8个顶点处分别标上1,2,3,4,5,6,7,8,然后再把每条棱两端所标的两个数之和写在这条棱的中点,问各棱中点所写的数是否可能恰有五种不同数值?各棱中点所写的数是否可能恰有四种不同数值?如果可能,对照如图在表中填上正确的数字;如果不可能,说明理由.
在正方体的8个顶点处分别标上1,2,3,4,5,6,7,8,然后再把每条棱两端所标的两个数之和写在这条棱的中点,问各棱中点所写的数是否可能恰有五种不同数值?各棱中点所写的数是否可能恰有四种不同数值?如果可能,对照如图在表中填上正确的数字;如果不可能,说明理由.| 不同数值 | A | B | C | D | E | F | G | H |
| 6,8,9,10,12 | 1 | 5 | 3 | 7 | 8 | 4 | 6 | 2 |
分析:各棱中点处所写的数恰有五种不同数值是可能的,如在A、B、…、H依次填1,5、3、7、8、4、6、2,则中点处恰有五个不同数值6、8、9、10、12.不可能少于五种不同数值,理由如下:
以1所在顶点为端点的棱有三条,不妨设这三条棱的另一端点所填写的数是a、b、c,满足a<b<c,则这三条棱的中点处的数为1+a,1+b和1+c,满足1+a<1+b<1+c.
以8所在顶点为端点的棱也有三条,不妨设这三条棱另一端点所填写的数为x、y、2,满足x<y<z,则这三条棱的中点处的数为8+x,8+y,8+z,满足8+x<8+y<8+z.
又 c≤8,1+c≤9;x≥1,8+x≥9,所以 1+a<1+b<1+c≤8+x<8+y<8+z,从而这六条棱中点的六个数不可能少于五种不同的值,因此在12条棱中的点处所写的数不可能有少于五种不同的数值.
以1所在顶点为端点的棱有三条,不妨设这三条棱的另一端点所填写的数是a、b、c,满足a<b<c,则这三条棱的中点处的数为1+a,1+b和1+c,满足1+a<1+b<1+c.
以8所在顶点为端点的棱也有三条,不妨设这三条棱另一端点所填写的数为x、y、2,满足x<y<z,则这三条棱的中点处的数为8+x,8+y,8+z,满足8+x<8+y<8+z.
又 c≤8,1+c≤9;x≥1,8+x≥9,所以 1+a<1+b<1+c≤8+x<8+y<8+z,从而这六条棱中点的六个数不可能少于五种不同的值,因此在12条棱中的点处所写的数不可能有少于五种不同的数值.
解答:解:因为以1所在顶点为端点的棱有三条,不妨设这三条棱的另一端点所填写的数是a、b、c,满足a<b<c,
则这三条棱的中点处的数为1+a,1+b和1+c,满足1+a<1+b<1+c.
以8所在顶点为端点的棱也有三条,不妨设这三条棱另一端点所填写的数为x、y、2,满足x<y<z,
则这三条棱的中点处的数为8+x,8+y,8+z,满足8+x<8+y<8+z.
又 c≤8,1+c≤9;x≥1,8+x≥9,
所以,1+a<1+b<1+c≤8+x<8+y<8+z
从而这六条棱中点的六个数不可能少于五种不同的值,因此在12条棱中的点处所写的数不可能有少于五种不同的数值.
则这三条棱的中点处的数为1+a,1+b和1+c,满足1+a<1+b<1+c.
以8所在顶点为端点的棱也有三条,不妨设这三条棱另一端点所填写的数为x、y、2,满足x<y<z,
则这三条棱的中点处的数为8+x,8+y,8+z,满足8+x<8+y<8+z.
又 c≤8,1+c≤9;x≥1,8+x≥9,
所以,1+a<1+b<1+c≤8+x<8+y<8+z
从而这六条棱中点的六个数不可能少于五种不同的值,因此在12条棱中的点处所写的数不可能有少于五种不同的数值.
点评:解答本题的关键是设出以1和以8为所在顶点为端点的棱,进而依次得出棱的中点数,进而解决问题.

练习册系列答案
相关题目
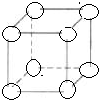 将1--8这八个整数放在正方体的八个顶点上,要求任一面上四个数之和都相等,请在如图正方体八个顶点处写出符合上述要求的一种填法.
将1--8这八个整数放在正方体的八个顶点上,要求任一面上四个数之和都相等,请在如图正方体八个顶点处写出符合上述要求的一种填法.