题目内容
 如图ABCD是个正方形,它的边长是4厘米,E、F分别是AB、BC的中点,图中阴影部分的面积是
如图ABCD是个正方形,它的边长是4厘米,E、F分别是AB、BC的中点,图中阴影部分的面积是6
6
平方厘米.分析:阴影部分是一个梯形,但是条件不足,没法直接利用梯形面积公式进行计算,根据题干可知正方形的面积为:4×4=16平方厘米,那么对角线AC就把这个正方形分成了面积相等的两个三角形,所以可得△ABC的面积为16÷2=8平方厘米,那么只要再求出△BEF的面积即可得到阴影部分的面积,根据已知条件”E、F分别是边AB、BC的中点”可得:△BEF与△ABC相似,相似比是1:2,由此即可求得△BEF的面积从而解决问题.
解答:解:根据题干分析可得:
△ABC的面积为:4×4÷2=8(平方厘米),
又因为在正方形ABCD中,E、F分别是边AB、BC的中点,
所以△BEF与△ABC相似,相似比是1:2,
那么它们的面积的比是1:4,
所以△BEF的面积为:8÷4=2(平方厘米),
故阴影部分的面积是:8-2=6(平方厘米);
故答案为:6.
△ABC的面积为:4×4÷2=8(平方厘米),
又因为在正方形ABCD中,E、F分别是边AB、BC的中点,
所以△BEF与△ABC相似,相似比是1:2,
那么它们的面积的比是1:4,
所以△BEF的面积为:8÷4=2(平方厘米),
故阴影部分的面积是:8-2=6(平方厘米);
故答案为:6.
点评:此题考查了运用相似三角形的判定与性质以及正方形一条对角线把正方形分成面积相等的两个三角形的性质的解决计算图形面积的方法.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 如图,两个正方形ABCD和GCEF它们的边长分别是6厘米与4厘米,求图中阴影部分的面积.
如图,两个正方形ABCD和GCEF它们的边长分别是6厘米与4厘米,求图中阴影部分的面积. 右图ABCD是个正方形,它的边长是8厘米,E、F分别是边AB、BC的中点,图中阴影部分的面积是
右图ABCD是个正方形,它的边长是8厘米,E、F分别是边AB、BC的中点,图中阴影部分的面积是
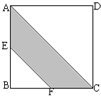 如图ABCD是个正方形,它的边长是4厘米,E、F分别是AB、BC的中点,图中阴影部分的面积是________平方厘米.
如图ABCD是个正方形,它的边长是4厘米,E、F分别是AB、BC的中点,图中阴影部分的面积是________平方厘米.